
【题目】如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=![]() .
.
(1)求证:AO⊥平面BCD;
(2)求异面直线AB与CD所成角的大小;
(3)求二面角O﹣AC﹣D的大小.

【答案】(1)证明过程详见解析(2)![]() (3)
(3)![]()
【解析】
(1)设![]() 是
是![]() 的中点,由等腰三角形的性质可得
的中点,由等腰三角形的性质可得![]() ,根据勾股定理可证明
,根据勾股定理可证明![]() ,从而证明
,从而证明![]() 平面
平面![]() ;(2)利用公式
;(2)利用公式![]()
![]() ,直接求异面直线
,直接求异面直线![]() 与
与![]() 所成角的的余弦值,然后求出角的大小;(3)利用射影面的面积与被射影面的面积的比,求二面角
所成角的的余弦值,然后求出角的大小;(3)利用射影面的面积与被射影面的面积的比,求二面角![]() 的余弦值,从而可得二面角的大小.
的余弦值,从而可得二面角的大小.
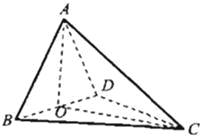
(1)设O是等腰直角三角形ABD斜边BD的中点,
所以有AO⊥BD,可求得AO=1,CO=![]() ,又有AC=2
,又有AC=2
所以∠AOC=90°,即AO⊥CO
BD,CO是平面BCD内两条相交直线,故有AO⊥平面BCD.
(2)由(1)可知BD⊥面AOC,
所以面BCD⊥面AOC,AO=1,CO=![]() ,AC=2
,AC=2
A点在BCD面内的投影为O,
cos<AB,CD>=cos∠ABDcos∠BDC=![]() =
=![]()
异面直线AB与CD所成角的大小为:arccos![]() .
.
(3)三角形AOC的面积为:![]() =
=![]() ;三角形ADC的面积为:
;三角形ADC的面积为:![]() =
=![]() ;
;
所以二面角O﹣AC﹣D的余弦为: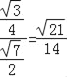 ,
,
二面角O﹣AC﹣D的大小为:arccos![]() .
.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
(1)求椭圆C的方程;
(2)是否存在直线l,满足![]() ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲乙两地某月12时的气温状况,选取该月5天中12时的气温数据(单位:![]() )制成如图所示的茎叶图,考虑以下结论:
)制成如图所示的茎叶图,考虑以下结论:

①甲地该月12时的平均气温低于乙地该月12时的平均气温;
②甲地该月12时的平均气温高于乙地该月12时的平均气温;
③甲地该月12时的气温的标准差小于乙地该月12时的气温的标准差;
④甲地该月12时的气温的标准差大于乙地该月12时的气温的标准差.
其中根据茎叶图能得到的统计结论的编号为( )
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的最小值为-1,且关于
的最小值为-1,且关于![]() 的方程
的方程![]() 的两根为0和-2.
的两根为0和-2.
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() 其中
其中![]() ,求函数
,求函数![]() 在
在![]() 时的最大值
时的最大值![]() ;
;
(3)若![]() (
(![]() 为实数),对任意
为实数),对任意![]() ,总存在
,总存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() ,称圆
,称圆![]() 为椭圆
为椭圆![]() 的“伴随圆”.已知点
的“伴随圆”.已知点![]() 是椭圆
是椭圆![]() 上的点
上的点
(1)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,求
有且只有一个公共点,求![]() 被椭圆
被椭圆![]() 的伴随圆
的伴随圆![]() 所截得的弦长:
所截得的弦长:
(2)![]() 是椭圆
是椭圆![]() 上的两点,设
上的两点,设![]() 是直线
是直线![]() 的斜率,且满足
的斜率,且满足![]() ,试问:直线
,试问:直线![]() 是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由。
是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于三次函数![]() ,定义
,定义![]() 是
是![]() 的导函数
的导函数![]() 的导函数,经过讨论发现命题:“一定存在实数
的导函数,经过讨论发现命题:“一定存在实数![]() ,使得
,使得![]() 成立”为真,请你根据这一结论判断下列命题:
成立”为真,请你根据这一结论判断下列命题:
①一定存在实数![]() ,使得
,使得![]() 成立;②一定存在实数
成立;②一定存在实数![]() ,使得
,使得![]() 成立;③若
成立;③若![]() ,则
,则![]() ;④若存在实数
;④若存在实数![]() ,且
,且![]() 满足:
满足:![]() ,则函数
,则函数![]() 在
在![]() 上一定单调递增,所有正确的序号是( )
上一定单调递增,所有正确的序号是( )
A. ①② B. ①③ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知动点![]() 都在曲线
都在曲线![]() (
(![]() 为参数,
为参数,![]() 是与
是与![]() 无关的正常数)上,对应参数分别为
无关的正常数)上,对应参数分别为![]() 与
与![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)作一个伸压变换:![]() ,求出动点
,求出动点![]() 点的参数方程,并判断动点
点的参数方程,并判断动点![]() 的轨迹能否过点
的轨迹能否过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北![]() 的方向上,仰角为
的方向上,仰角为![]() ,行驶4km后到达B处,测得此山顶在西偏北
,行驶4km后到达B处,测得此山顶在西偏北![]() 的方向上.
的方向上.
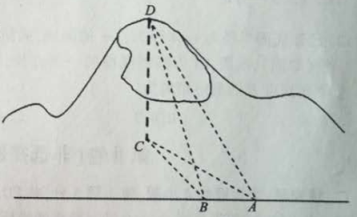
(1)求此山的高度(单位:km);
(2)设汽车行驶过程中仰望山顶D的最大仰角为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com