
【题目】[选修4-4:坐标系与参数方程]
已知动点![]() 都在曲线
都在曲线![]() (
(![]() 为参数,
为参数,![]() 是与
是与![]() 无关的正常数)上,对应参数分别为
无关的正常数)上,对应参数分别为![]() 与
与![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)作一个伸压变换:![]() ,求出动点
,求出动点![]() 点的参数方程,并判断动点
点的参数方程,并判断动点![]() 的轨迹能否过点
的轨迹能否过点![]() .
.
科目:高中数学 来源: 题型:
【题目】某公园举办雕塑展览吸引着四方宾客,旅游人数![]() 与人均消费
与人均消费![]() (元)的关系如下:
(元)的关系如下: .
.
(1)若游客客源充足,那么当天接待游客多少人时,公园的旅游收入最多?
(2)若公园每天运营成本为5万元(不含工作人员的工资),还要上缴占旅游收入![]() 的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有![]() 四个景点,一位游客来该市游览,已知该游客游览
四个景点,一位游客来该市游览,已知该游客游览![]() 的概率为
的概率为![]() ,游览
,游览![]() 、
、![]() 和
和![]() 的概率都是
的概率都是![]() ,且该游客是否游览这四个景点相互独立.
,且该游客是否游览这四个景点相互独立.
(1)求该游客至多游览一个景点的概率;
(2)用随机变量![]() 表示该游客游览的景点的个数,求
表示该游客游览的景点的个数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光农业科学研究所对冬季昼夜温差大小与反季节土豆发芽多少之间的关系进行分析研究,他们分别记录了11月1日至11月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如表资料:
日期 | 11月1日 | 11月2日 | 11月3日 | 11月4日 | 11月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 26 | 32 | 26 | 16 |
设农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是11月1日与11月5日的两组数据,请根据11月2日至11月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 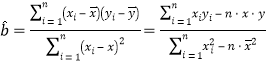 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元,甲、乙电视台的广告费标准分别是500元/分钟和200元分钟,假设甲、乙两个电视台为该公司做的广告能给公司带来的收益分别为0.4万元/分钟和0.2万元分钟,那么该公司合理分配在甲、乙两个电视台的广告时间,能使公司获得最大的收益是()万元
A.72B.80C.84D.90
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com