Question

【题目】【江西省临川实验学校2017届高三第一次模拟考试数学（文）】已知抛物线，焦点为，点在抛物线上，且到的距离比到直线的距离小1.

（1）求抛物线的方程；

（2）若点为直线上的任意一点，过点作抛物线的切线与，切点分别为，求证:直线恒过某一定点.

Answer 1

【答案】（1）（2）

【解析】试题分析：（1）根据抛物线定义可得直线为抛物线的准线，即得，（2）关键求出直线AB方程，先设切点的坐标，利用导数几何意义可得切线斜率，进而根据点斜式可得切线方程，求两切线方程交点可得点坐标，由于点在直线上，所以可得.最后联立AB方程与抛物线方程，利用韦达定理得，即得直线恒过定点.

试题解析：（1）因为到的距离与到直线的距离相等，由拋物线定义知，直线为抛物线的准线，所以，得,所以抛物线的方程为.

（2）设切点的坐标分别为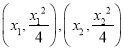，由(1)知， .

则切线的斜率分别为,,

故切线 的方程分别为, ,

联立以上两个方程，得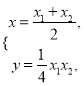故的坐标为.

因为点在直线上，所以，即.

设直线的方程为，代入抛物线方程，得，所以，即，所以.

故的方程为,故直线恒过定点.