
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(Ⅰ)解不等式: ![]() ;
;
(Ⅱ)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴围成一个三角形,求实数
轴围成一个三角形,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)由已知,可按不等中两个绝对值式的零点将实数集分为三部分进行分段求解,然后再综合其所得解,从而求出所求不等式的解集;
(Ⅱ)由题意,可将![]() 的值分为
的值分为![]() 和
和![]() 进行分类讨论,当
进行分类讨论,当![]() 时,函数
时,函数![]() 不过原点,且最小值为
不过原点,且最小值为![]() ,此时满足题意;当
,此时满足题意;当![]() 时,函数
时,函数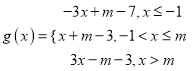 ,再由函数
,再由函数![]() 的单调性及值域,求出实数
的单调性及值域,求出实数![]() 的范围,最后综合两种情况,从而得出实数
的范围,最后综合两种情况,从而得出实数![]() 的范围.
的范围.
试题解析:(Ⅰ)由题意知,原不等式等价于
![]() 或
或![]() 或
或![]() ,
,
解得![]() 或
或![]() 或
或![]() ,
,
综上所述,不等式![]() 的解集为
的解集为![]() .
.
(Ⅱ)当![]() 时,则
时,则![]()
![]() ,
,
此时![]() 的图象与
的图象与![]() 轴围成一个三角形,满足题意:
轴围成一个三角形,满足题意:
当![]() 时,
时, ![]()
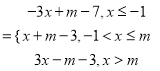 ,
,
则函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
要使函数![]() 的图象与
的图象与![]() 轴围成一个三角形,
轴围成一个三角形,
则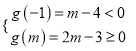 ,解得
,解得![]() ;
;
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】在即将进入休渔期时,某小微企业决定囤积一些冰鲜产品,销售所囤积产品的净利润f(x)万元与投入x万元之间近似满足函数关系: ,若投入2万元,可得到净利润为5.2万元.
,若投入2万元,可得到净利润为5.2万元.
(1)试求该小微企业投入多少万元时,获得的净利润最大;
(2)请判断该小微企业是否会亏本,若亏本,求出投入资金的范围,若不亏本,请说明理由.(参考数据:ln 2≈0.7,ln 15≈2.7)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图,估计这次数学竞赛的及格率(60分及以上为及格)是( )

A. 0.9 B. 0.75 C. 0.8 D. 0.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为3的等边三角形,四边形
是边长为3的等边三角形,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .点
.点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,点
,点![]() 为
为![]() 上的一点,且
上的一点,且![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,在直四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA
中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA![]() =2,E、E
=2,E、E![]() 分别是棱AD、AA
分别是棱AD、AA![]() 的中点.
的中点.

(1)设F是棱AB的中点,证明:直线EE![]() //平面FCC
//平面FCC![]() ;
;
(2)证明:平面D1AC⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下四种变换方式:
① 向左平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
② 向右平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
③ 每个点的横坐标缩短为原来的![]() ,向右平移
,向右平移![]() 个单位长度;
个单位长度;
④ 每个点的横坐标缩短为原来的![]() ,向左平移
,向左平移![]() 个单位长度;
个单位长度;
其中能将![]() 的图像变换成函数
的图像变换成函数![]() 的图像的是( )
的图像的是( )
A.①和③ B.①和④ C.②和④ D.②和③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底,
为自然对数的底, ![]() )的导函数为
)的导函数为![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)设点![]() ,
, ![]() 是函数
是函数![]() 图象上两点,若对任意的
图象上两点,若对任意的![]() ,割线
,割线![]() 的斜率都大于
的斜率都大于![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 为椭圆
为椭圆![]() 的左焦点,离心率为
的左焦点,离心率为![]() ,直线
,直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是弦
是弦![]() 的中点,
的中点,![]() 是椭圆
是椭圆![]() 上一点,求
上一点,求![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com