练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．在（x2+2x+y）5的展开式中，x5y2的系数为60．

    分析 把（x2+2x+y）5化简成二项式机构，利用通项公式可得答案．

    解答 解：由（x2+2x+y）5化简为[x2+2x）+y]，
    由通项公式Tr+1=${C}_{5}^{r}{y}^{r}（{x}^{2}+2x）^{5-r}$，要出现y2，∴r=2．
    二项式（x2+2x）3展开式中出现x5．
    由通项公式Tk+1=${C}_{3}^{k}{x}^{2（3-k）}{2}^{k}{x}^{k}$，
    ∴2（3-k）+k=5，
    可得：k=1．
    ∴x5y2的系数为${C}_{5}^{2}×2{×C}_{3}^{1}$=60．
    故答案为：60．

    点评 本题主要考查二项式定理对三项式的处理能力的应用，考查了二项式系数的性质，二项式展开式的通项公式，体现了转化的数学思想，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知f（x）是二次函数，不等式f（x）＜0的解集为（0，5），且f（x）在[-1，4]上的最大值是12．
    （1）求f（x）的解析式；
    （2）是否存在自然数m，使得方程$f（x）+\frac{37}{x}=0$在区间（m，m+1）内有且只有两个不等的实根？若存在，求出m的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设z=$\frac{（1-4i）（1+i）+2+4i}{3+4i}$．
    ①求|z|；
    ②若$\frac{{|{\overline z}|+mi}}{1-i}=\sqrt{2}$i，m∈R，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知复数Z为纯虚数，若（z+2）2-8i也是纯虚数，则Z的虚部为（　　）
    A．2B．-2C．-2iD．2或-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知α是第三象限角，$f（α）=\frac{sin（π-α）cos（2π-α）tan（-α-π）}{tan（-α）sin（-π-α）}$
    （1）化简f（α）；
    （2）若$cos（α-\frac{3π}{2}）=\frac{1}{5}$，求f（α）的值；．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．某程序框图如图所示，若输入的n=10，则输出结果为（　　）
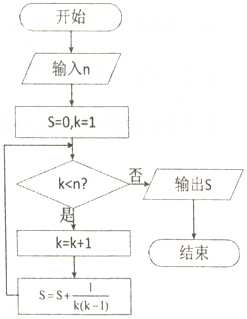
    A．$\frac{1}{10}$B．$\frac{8}{9}$C．$\frac{9}{10}$D．$\frac{10}{11}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知复数z满足（1+2i3）z=1+2i，则z的虚部是$\frac{4}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但采集上市时蔬菜仍存有少量的残留农药，食用时需要用清水清洗干净，下表是用清水x（单位：千克） 清洗该蔬菜1千克后，蔬菜上残留的农药y（单位：微克） 的统计表：
    x12345
     y5854392910
    （1）在下面的坐标系中，描出散点图，并判断变量x与y的相关性；
    （2）若用解析式$\widehaty=c{x^2}+d$作为蔬菜农药残量$\widehaty$与用水量x的回归方程，令ω=x2，计算平均值$\overlineω$与$\overline y$，完成以下表格（填在答题卡中），求出$\widehaty$与x的回归方程．（c，d精确到0.1）
    ω1491625
    y5854392910
    ${ω_i}-\overlineω$-10-7-2514
    ${y_i}-\overline y$20161-28
    （3）对于某种残留在蔬菜上的农药，当它的残留量低于20微克时对人体无害，为了放心食用该蔬菜，请
    估计需要用多少千克的清水清洗一千克蔬菜？（精确到0.1，参考数据$\sqrt{5}≈2.236$）
    （附：线性回归方程$\widehaty=bx+a$中系数计算公式分别为；$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$a=\overline y-b\overline x$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．椭圆的中心在坐标原点，焦点在x轴上，左右顶点分别为A1、A2，上下顶点分别为B1、B2，F2为右焦点，延长B2F2与A2B1交于点P，若∠B2PA2为钝角，则该椭圆离心率的取值范围是（　　）
    A．$（{\frac{{\sqrt{5}-2}}{2}，0}）$B．$（{0，\frac{{\sqrt{5}-2}}{2}}）$C．$（{0，\frac{{\sqrt{5}-1}}{2}}）$D．$（{\frac{{\sqrt{5}-1}}{2}，1}）$

    查看答案和解析>>

    同步练习册答案