
如图,已知圆E 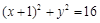 ,点
,点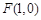 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(1)求动点Q的轨迹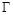 的方程;
的方程;
(2)点 ,
,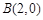 ,点G是轨迹
,点G是轨迹 上的一个动点,直线AG与直线
上的一个动点,直线AG与直线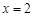 相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.
相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.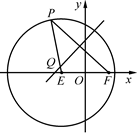
(1)点Q的轨迹 的方程为为
的方程为为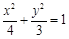 .(2)以线段BD为直径的圆与直线GF相切.
.(2)以线段BD为直径的圆与直线GF相切.
解析试题分析:(1)连结QF,由于线段的垂直平分线上的点到线段两端点的距离相等,所以|QE|+|QF|=|QE|+|QP|=4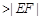 ,根据椭圆的定义知,动点Q的轨迹
,根据椭圆的定义知,动点Q的轨迹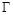 是以E,F为焦点,长轴长为4的椭圆.由此便可得其方程;(2)直线与圆的位置关系一般通过比较圆心到直线的距离与圆的半径的大小关系来确定. 由题意,设直线AG的方程为
是以E,F为焦点,长轴长为4的椭圆.由此便可得其方程;(2)直线与圆的位置关系一般通过比较圆心到直线的距离与圆的半径的大小关系来确定. 由题意,设直线AG的方程为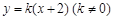 ,则点D坐标为
,则点D坐标为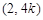 ,由此可得圆心和半径.下面用k表示点G的坐标,求出直线GF方程为
,由此可得圆心和半径.下面用k表示点G的坐标,求出直线GF方程为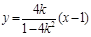 ,进而求到圆心到直线GF的距离便可知道以BD为直径的圆与直线GF的位置关系.
,进而求到圆心到直线GF的距离便可知道以BD为直径的圆与直线GF的位置关系.
(1)连结QF,根据题意,|QP|=|QF|,
则|QE|+|QF|=|QE|+|QP|=4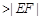 ,
,
故Q的轨迹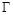 是以E,F为焦点,长轴长为4的椭圆. .2分
是以E,F为焦点,长轴长为4的椭圆. .2分
设其方程为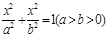 ,可知
,可知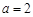 ,
,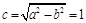 ,则
,则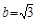 , ..3分
, ..3分
所以点Q的轨迹 的方程为为
的方程为为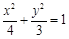 . 4分
. 4分
(2)以线段BD为直径的圆与直线GF相切. 5分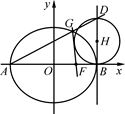
由题意,设直线AG的方程为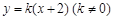 ,则点D坐标为
,则点D坐标为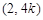 ,BD的中点H的坐标为
,BD的中点H的坐标为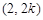 .
.
联立方程组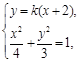 消去y得
消去y得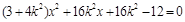 ,
,
设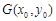 ,则
,则 ,
,
所以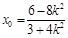 ,
, , 7分
, 7分
当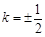 时,点G的坐标为
时,点G的坐标为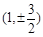 ,点D的坐标为
,点D的坐标为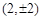 .
.
直线GF⊥x轴,此时以BD为直径的圆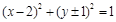 与直线GF相切. 9分
与直线GF相切. 9分
当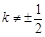 时,则直线GF的斜率为
时,则直线GF的斜率为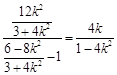 ,则直线GF方程为
,则直线GF方程为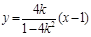 ,
,
点H到直线GF的距离 ,又
,又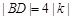 ,
,
所以圆心H到直线GF的距离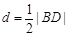 ,此时,以BD为直径的圆与直线GF相切.
,此时,以BD为直径的圆与直线GF相切.
综上所述,以线段BD为直径的圆与直线GF相切. 13分
考点:1、椭圆的方程;2、直线与椭圆的关系;3、最值问题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
在平面直角坐标系 中,原点为
中,原点为 ,抛物线
,抛物线 的方程为
的方程为 ,线段
,线段 是抛物线
是抛物线 的一条动弦.
的一条动弦.
(1)求抛物线 的准线方程和焦点坐标
的准线方程和焦点坐标 ;
;
(2)若 ,求证:直线
,求证:直线 恒过定点;
恒过定点;
(3)当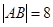 时,设圆
时,设圆 ,若存在且仅存在两条动弦
,若存在且仅存在两条动弦 ,满足直线
,满足直线 与圆
与圆 相切,求半径
相切,求半径 的取值范围?
的取值范围?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系xOy中,已知点A(0,-1),B点在直线y = -3上,M点满足 ,
, 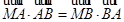 ,M点的轨迹为曲线C。
,M点的轨迹为曲线C。
(1)求C的方程;
(2)P为C上的动点,l为C在P点处得切线,求O点到l距离的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设椭圆C1: =1(a>b>0)的左、右焦点分别为为
=1(a>b>0)的左、右焦点分别为为 ,
, 恰是抛物线C2:
恰是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
的焦点,点M为C1与C2在第一象限的交点,且|MF2|= .
.
(1)求C1的方程;
(2)平面上的点N满足 ,直线l∥MN,且与C1交于A,B两点,若
,直线l∥MN,且与C1交于A,B两点,若 ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
长方形 中,
中,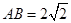 ,
,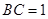 .以
.以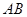 的中点
的中点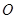 为坐标原点,建立如图所示的直角坐标系.
为坐标原点,建立如图所示的直角坐标系.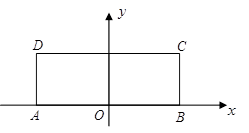
(1) 求以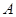 、
、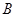 为焦点,且过
为焦点,且过 、
、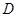 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2) 过点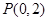 的直线
的直线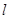 交(1)中椭圆于
交(1)中椭圆于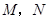 两点,是否存在直线
两点,是否存在直线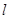 ,使得以线段
,使得以线段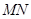 为直径的圆恰好过坐标原点?若存在,求出直线
为直径的圆恰好过坐标原点?若存在,求出直线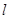 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,设抛物线 :
: 的焦点为
的焦点为 ,准线为
,准线为 ,过准线
,过准线 上一点
上一点 且斜率为
且斜率为 的直线
的直线 交抛物线
交抛物线 于
于 ,
, 两点,线段
两点,线段 的中点为
的中点为 ,直线
,直线 交抛物线
交抛物线 于
于 ,
, 两点.
两点.
(1)求抛物线 的方程及
的方程及 的取值范围;
的取值范围;
(2)是否存在 值,使点
值,使点 是线段
是线段 的中点?若存在,求出
的中点?若存在,求出 值,若不存在,请说明理由.
值,若不存在,请说明理由. 
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知 ,
, ,
, ,
, 分别是椭圆
分别是椭圆 的四个顶点,△
的四个顶点,△ 是一个边长为2的等边三角形,其外接圆为圆
是一个边长为2的等边三角形,其外接圆为圆 .
.
(1)求椭圆 及圆
及圆 的方程;
的方程;
(2)若点 是圆
是圆 劣弧
劣弧 上一动点(点
上一动点(点 异于端点
异于端点 ,
, ),直线
),直线 分别交线段
分别交线段 ,椭圆
,椭圆 于点
于点 ,
, ,直线
,直线 与
与 交于点
交于点 .
.
(ⅰ)求 的最大值;
的最大值;
(ⅱ)试问:. .,
., 两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设椭圆C1: 的右焦点为F,P为椭圆上的一个动点.
的右焦点为F,P为椭圆上的一个动点.
(1)求线段PF的中点M的轨迹C2的方程;
(2)过点F的直线l与椭圆C1相交于点A、D,与曲线C2顺次相交于点B、C,当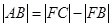 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com