
【题目】如图, 平面![]() 平面
平面![]() 为等边三角形,
为等边三角形,![]() , 过
, 过![]() 作平面交
作平面交![]() 分别于点
分别于点![]() ,设
,设![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 的值, 使得平面
的值, 使得平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() .
.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需结合平几条件,如三角形相似,本题可根据![]() 得
得![]() ,而
,而![]() ,因此
,因此![]() (2)利用空间向量研究二面角,首先利用垂直关系建立恰当的空间直角坐标系,设立各点坐标,利用方程组解两个平面的法向量,利用向量数量积求夹角,最后根据向量夹角与二面角之间关系得等量关系,求
(2)利用空间向量研究二面角,首先利用垂直关系建立恰当的空间直角坐标系,设立各点坐标,利用方程组解两个平面的法向量,利用向量数量积求夹角,最后根据向量夹角与二面角之间关系得等量关系,求![]() 的值
的值
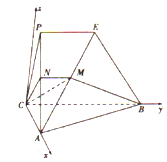
试题解析:(1)证明:如图, 以点![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,不妨设
,不妨设![]() ,则
,则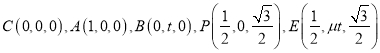 ,
,
由 ![]() ,得
,得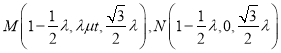 ,则
,则![]() .易知
.易知![]() 是平面
是平面![]() 的一个法向量, 且
的一个法向量, 且![]() ,故
,故![]() ,又因为
,又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(2)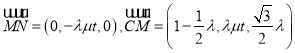 ,设平面
,设平面![]() 法向量为
法向量为![]() ,则
,则![]() ,故可取
,故可取![]() ,又
,又![]() 是平面
是平面![]() 的一个法向量, 由
的一个法向量, 由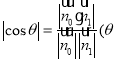 为平面
为平面![]() 与平面
与平面![]() 所成锐二面角的度数), 以及
所成锐二面角的度数), 以及![]() 得,
得,![]() . 解得
. 解得![]() 或
或![]() (舍去), 故
(舍去), 故![]() .
.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】如图所示,ABCD为矩形,PA⊥平面ABCD,PA=AD,M,N,Q分别是PC,AB,CD的中点.

求证:(1)MN∥平面PAD;
(2)平面QMN∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当a=1时,求函数f(x)在[1,e]上的最小值和最大值;
(2)当a≤0时,讨论函数f(x)的单调性;
(3)是否存在实数a,对任意的x1,x2![]() (0,+∞),且x1≠x2,都有
(0,+∞),且x1≠x2,都有![]() 恒成立.若存在,求出a的取值范围;若不存在,说明理由.
恒成立.若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 为椭圆
为椭圆![]() 的左顶点,点
的左顶点,点![]() 为椭圆
为椭圆![]() 的上顶点,且
的上顶点,且![]() .
.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,证明:点
,证明:点![]() 在直线
在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若b2-4ac<0,则方程ax2+bx+c=0(a≠0)没有实根”的否命题;
②命题“在△ ABC中,若AB=BC=CA,则△ ABC为等边三角形”的逆命题;
③命题“若a>b>0,则![]() a>
a>![]() b>0”的逆否命题;
b>0”的逆否命题;
④命题“若m>1,则mx2-2(m+1)x+(m-3)<0的解集为R”的逆命题.
其中真命题的序号为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通部门对某路段公路上行驶的汽车速度实施监控,从速度在50﹣90km/h的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在70km/h以下的汽车有辆.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“t≠0,mt=ntm=n”类比得到“c≠0,a·c=b·ca=b”;
④“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑤“(m·n)t=m(n·t)”类比得到“(a·b)·c=a(b·c)”;
⑥“![]() ”类比得到
”类比得到![]() .以上的式子中,类比得到的结论正确的是________.
.以上的式子中,类比得到的结论正确的是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com