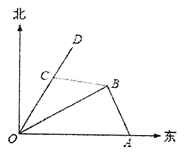
【题目】如图，港口
在港口
的正东120海里处，小岛
在港口的北偏东
的方向，且在港口北偏西
的方向上，一艘科学考察船从港口出发，沿北偏东的
方向以20海里/小时的速度驶离港口.一艘给养快艇从港口以60海里/小时的速度驶向小岛，在岛转运补给物资后以相同的航速送往科考船.已知两船同时出发，补给装船时间为1小时.
（1）求给养快艇从港口到小岛的航行时间；
（2）给养快艇驶离港口后，最少经过多少小时能和科考船相遇？
【答案】（1）快艇从港口
到小岛
的航行时间为
小时（2）给养快艇驶离港口后，最少经过3小时能和科考船相遇
【解析】
（1）给养快艇从港口到小岛的航行时间，已知其速度，则只要求得
的路程，再利用路程公式即可求得所需的时间．
（2）由（1）知，给养快艇从港口驶离2小时后，从小岛出发与科考船汇合，根据题意确定各边长和各角的值，然后由余弦定理解决问题．
（1）由题意知，在
中，
，
，
，
所以
，
于是
，
而快艇的速度为
海里/小时，
所以快艇从港口到小岛的航行时间为
小时.
（2）由（1）知，给养快艇从港口驶离2小时后，从小岛出发与科考船汇合.为使航行的时间最少，快艇从小岛驶离后必须按直线方向航行，
设给养快艇驶离港口
小时后恰与科考船在
处相遇.
在中，
，
而在
中，
，
，
，
由余弦定理，得
，
即
，
化简，得
，
解得
或
（舍去）.
故
.
即给养快艇驶离港口后，最少经过3小时能和科考船相遇.
科目：高中数学 来源： 题型：
【题目】如图，在棱长为
的正方体
中，
，
分别是
和
的中点．
（
）求异面直线
与
所成角的余弦值．
（）在棱
上是否存在一点
，使得二面角
的大小为
？若存在，求出
的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
：
的焦点为
，点
为上异于顶点的任意一点，过的直线
交于另一点
，交
轴正半轴于点
，且有
，当点的横坐标为3时，
为正三角形.
（1）求的方程；
（2）若直线
，且
和相切于点
，试问直线
是否过定点，若过定点，求出定点坐标；若不过定点，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以下四个命题：
①“若
，则
”的逆否命题为真命题
②“
”是“函数
在区间
上为增函数”的充分不必要条件
③若
为假命题，则
，
均为假命题
④对于命题：
，
，则
为：
，
其中真命题的个数是（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C：
的左、右顶点分别为A，B，离心率为
，点P（1，
）为椭圆上一点．
（1）求椭圆C的标准方程；
（2）如图，过点C（0，1）且斜率大于1的直线l与椭圆交于M，N两点，记直线AM的斜率为k1，直线BN的斜率为k2，若k1=2k2，求直线l斜率的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
