
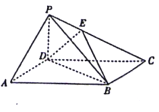
【题目】如图所示,在四棱锥![]() 中,底要
中,底要![]() 为平行四边形,
为平行四边形, ![]() ,
,
![]() ,
, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.
(1)证明: ![]() ;
;
(2)求二面角![]() 余弦值.
余弦值.
【答案】(1)详见解析(2)![]()
【解析】试题分析:(1)由![]() 底面
底面![]() ,得
,得![]() ,再利用余弦定理计算AD,根据勾股定理得
,再利用余弦定理计算AD,根据勾股定理得![]() ,利用线面垂直判定定理可得
,利用线面垂直判定定理可得![]() ,最后根据线面垂直性质定理得
,最后根据线面垂直性质定理得![]() ;(2)利用空间向量数量积求二面角的余弦值,先根据条件建立恰当空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据二面角与法向量夹角关系确定所求值.
;(2)利用空间向量数量积求二面角的余弦值,先根据条件建立恰当空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据二面角与法向量夹角关系确定所求值.
试题解析:(1)证明:在![]() 中,
中, ![]() .
.
不妨设![]() ,则由已知
,则由已知![]() ,得
,得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,又
,又![]() 底面
底面![]() ,所以
,所以![]()
所以 .
.
(2)解:由(1)知![]() ,
, ![]() ,以
,以![]() 为原点,如图所示建立空间直角坐标系
为原点,如图所示建立空间直角坐标系![]() ,设
,设![]() ,
,
于是![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
因为![]() 为
为![]() 上一点,且
上一点,且![]() ,所以
,所以![]() ,所以
,所以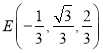 ,
,
所以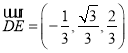 ,
,![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
则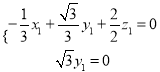 ,令
,令![]() ,则
,则![]()
又![]() ,
, ,设平面
,设平面![]() 的法向量
的法向量![]()
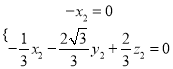 ,令
,令![]() ,则
,则![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,由图可知
,由图可知![]() ,则
,则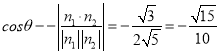 .
.


科目:高中数学 来源: 题型:
【题目】(文科)已知的椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,上顶点
,上顶点![]() ,
, ![]() 是正三角形且周长为6.
是正三角形且周长为6.
(1)求椭圆![]() 的标准方程及离心率;
的标准方程及离心率;
(2) ![]() 为坐标原点,
为坐标原点, ![]() 是直线
是直线![]() 上的一个动点,求
上的一个动点,求![]() 的最小值,并求出此时点
的最小值,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
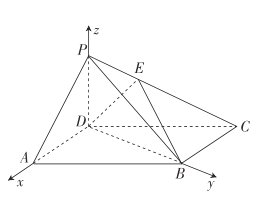
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,动点
,动点![]() ,
, ![]() 分别在
分别在![]() 轴,
轴, ![]() 轴上运动,
轴上运动, ![]() ,
, ![]() 为平面上一点,
为平面上一点, ![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() .
.
(Ⅰ)求点![]() 的轨迹曲线
的轨迹曲线![]() 的方程;
的方程;
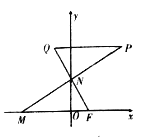
(Ⅱ)过![]() 点作
点作![]() 轴的垂线
轴的垂线![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() ,
, ![]() 分别交曲线
分别交曲线![]() 于
于![]() ,
, ![]() 两点(直线
两点(直线![]() 不过
不过![]() ),交
),交![]() 于
于![]() ,
, ![]() 两点.若线段
两点.若线段![]() 中点的轨迹方程为
中点的轨迹方程为![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定, ![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S7=0,a3﹣2a2=12.
(1)求数列{an}的通项公式;
(2)求Sn﹣15n+50的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=﹣ ![]() ,an+1=
,an+1= ![]() (n∈N+)
(n∈N+)
(1)证明数列{ ![]() }是等差数列并求{an}的通项公式.
}是等差数列并求{an}的通项公式.
(2)数列{bn}满足bn= ![]() (n∈N+).求{bn}的前n项和Sn .
(n∈N+).求{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品.为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如下表所示:
,如下表所示:

已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知变量![]() ,
, ![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC三个顶点坐标分别为:A(1,0),B(1,4),C(3,2),直线l经过点(0,4).
(1)求△ABC外接圆⊙M的方程;
(2)若直线l与⊙M相交于P,Q两点,且|PQ|=2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com