
【题目】设![]() 或
或![]() ,
,![]() ,若
,若![]() 是
是![]() 的充分条件.
的充分条件.
(1)求证:函数![]() 的图像总在直线
的图像总在直线![]() 的下方;
的下方;
(2)是否存在实数![]() ,使得不等式
,使得不等式![]() 对一切实数
对一切实数![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了治理大气污染,某市2017年初采用了一系列措施,比如“煤改电”,“煤改气”,“整治散落污染企业”等.下表是该市2016年11月份和2017年11月份的空气质量指数(![]() )(
)(![]() 指数越小,空气质量越好)统计表.根据表中数据回答下列问题:
指数越小,空气质量越好)统计表.根据表中数据回答下列问题:
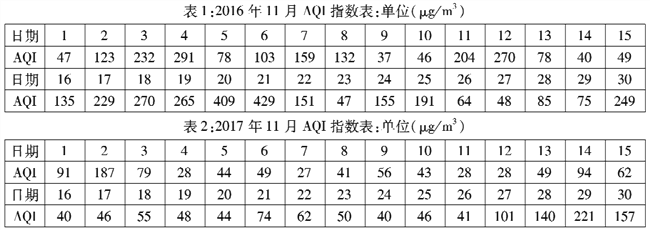
(1)将2017年11月的空气质量指数![]() 数据用该天的对应日期作为样本编号,再用系统抽样方法从中抽取6个
数据用该天的对应日期作为样本编号,再用系统抽样方法从中抽取6个![]() 数据,若在2017年11月16日到11月20日这五天中用简单随机抽样抽取到的样本的编号是19号,写出抽出的样本数据;
数据,若在2017年11月16日到11月20日这五天中用简单随机抽样抽取到的样本的编号是19号,写出抽出的样本数据;
(2)从(1)中抽出的6个样本数据中随机抽取2个,求这2个![]() 数据之差的绝对值小于30的概率;
数据之差的绝对值小于30的概率;
(3)根据《环境空气质量指数(![]() )技术规定(试行)》规定:当空气质量指数为
)技术规定(试行)》规定:当空气质量指数为![]() (含50)时,空气质量级别为一级,求出这两年11月空气质量指数为一级的概率,你认为该市2017年初开始采取的这些大气污染治理措施是否有效?
(含50)时,空气质量级别为一级,求出这两年11月空气质量指数为一级的概率,你认为该市2017年初开始采取的这些大气污染治理措施是否有效?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,M,O分别为CD和AC的中点,
,M,O分别为CD和AC的中点,![]() 平面ABCD.
平面ABCD.
![]() 求证:平面
求证:平面![]() 平面PAC;
平面PAC;
![]() Ⅱ
Ⅱ![]() 是否存在线段PM上一点N,使得
是否存在线段PM上一点N,使得![]() 平面PAB,若存在,求
平面PAB,若存在,求![]() 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
,![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 点处的切线方程;
点处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围;
的取值范围;
(3)求证:对于任意大于![]() 的正整数
的正整数![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算均值;
(2)试从两位考生正确完成题数的均值及至少正确完成2题的概率分析比较两位考生的实验操作能力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出一个球,在摸出的2个球中,若都是红球,则获得一等奖;若只有1个红球,则获得二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中或一等奖的次数为![]() ,求
,求![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com