
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值.经数据处理后得到该样本的频率分布直方图,其中质量指标值不大于1.50的茎叶图如图所示,以这100件产品的质量指标值在各区间内的频率代替相应区间的概率.
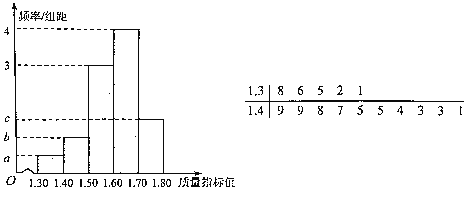
(1)求图中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计这种产品质量指标值的平均数及方差(说明:①同一组中的数据用该组区间的中点值作代表;②方差的计算只需列式正确);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于1.50的产品至少要占全部产品的![]() ”的规定?
”的规定?
【答案】(1) ![]() ,
,![]() ,
,![]() .(2)
.(2) ![]() ;
;![]() (3) 不能认为符合规定
(3) 不能认为符合规定
【解析】
(1)由频率分布直方图和茎叶图的性质列出方程组,能求出a,b,c.
(2)利用频率分布直方图能估计这种产品质量指标值的平均数和方差.
(3)质量指标值不低于1.50的产品占比为0.30+0.40+0.15=0.85<0.9,由此能求出结果.
解:解:(1)由频率分布直方图和茎叶图得:
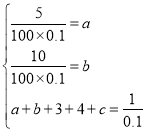 ,
,
解得a=0.5,b=1,c=1.5.
(2)估计这种产品质量指标值的平均数为:
![]() 1.35×0.5×0.1+1.45×1×0.1+1.55×3×0.1+1.65×4×0.1+1.75×1.5×0.1=1.6,
1.35×0.5×0.1+1.45×1×0.1+1.55×3×0.1+1.65×4×0.1+1.75×1.5×0.1=1.6,
估计这种产品质量指标值的方差为:
S2=(1.35﹣1.6)2×0.05+(1.45﹣1.6)2×0.1+(1.55﹣1.6)2×0.4+(1.75﹣1.6)2×0.15=0.0105.
(3)∵质量指标值不低于1.50的产品占比为:
0.30+0.40+0.15=0.85<0.9,
∴不能认为该企业生产的这种产品符合“质量指标值不低于1.50的产品至少要占全部产品的90%”的规定.


科目:高中数学 来源: 题型:
【题目】曲线![]() 的极坐标方程为
的极坐标方程为![]() (常数
(常数![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为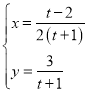 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和
的直角坐标方程和![]() 的普通方程;
的普通方程;
(2)若曲线![]() ,
,![]() 有两个不同的公共点,求实数
有两个不同的公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,且
,且![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 过焦点
过焦点![]() 且与抛物线交于
且与抛物线交于![]() 、
、![]() 两点,当直线
两点,当直线![]() 的倾斜角为30°时,
的倾斜角为30°时,![]() .
.
(1)求抛物线方程.
(2)在平面直角坐标系![]() 中,是否存在定点
中,是否存在定点![]() ,当直线
,当直线![]() 绕
绕![]() 旋转时始终都满足
旋转时始终都满足![]() 平分
平分![]() .若存在,求出
.若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的上顶点
的上顶点![]() 为圆心作圆,
为圆心作圆,
![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,在第二象限交于点
,在第二象限交于点![]() .
.
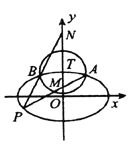
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求出此时圆
的最小值,并求出此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的一点,且直线
的一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 为坐标原点,求证:
为坐标原点,求证:
![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面的问题中,并解决该问题.
这三个条件中任选一个,补充在下面的问题中,并解决该问题.
已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ______________,
______________,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com