
【题目】已知函数![]() .
.
![]() 求
求![]() 的单调区间和极值;
的单调区间和极值;
![]() 当
当![]() 时,若
时,若![]() ,且
,且![]() ,证明:
,证明:![]() .
.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】2018年开始,直播答题突然就火了,在某场活动中,最终仅有23人平分100万奖金,这23人可以说是“学霸”级的大神.但随着直播答题的发展,其模式的可持续性受到了质疑,某网战随机选取500名网民进行了调查,得到的数据如下表:
男 | 女 | |
认为直播答题模式可持续 | 180 | 140 |
认为直播答题模式不可持续 | 120 | 60 |
(1)根据表格中的数据,用独立性检验的思维方法判断是否有97.5%的把握认为对直播答题模式的态度与性别有关系?
(2)已知在参与调查的500人中,有15%曾参加答题游戏瓜分过奖金,而男性被调查者有12%曾参加游戏瓜分过奖金,求女性被调查者参与游戏瓜分过奖金的概率.
参考公式:![]()
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的相邻两对称轴间的距离为
的相邻两对称轴间的距离为![]() ,若将
,若将![]() 的图像先向左平移
的图像先向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位,所得的函数
个单位,所得的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不等实根,求实数
上有两个不等实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答下列问题:
(1)求平行于直线3x+4y- 2=0,且与它的距离是1的直线方程;
(2)求垂直于直线x+3y -5=0且与点P( -1,0)的距离是![]() 的直线方程.
的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级学生会有理科生4名,其中3名男同学;文科生3名,其中有1名男同学.从这7名成员中随机抽4人参加高中示范校验收活动问卷调查.
(Ⅰ)设![]() 为事件“选出的4人中既有文科生又有理科生”,求事件
为事件“选出的4人中既有文科生又有理科生”,求事件![]() 的概率;
的概率;
(Ⅱ)设![]() 为选出的4人中男生人数与女生人数差的绝对值,求随机变量
为选出的4人中男生人数与女生人数差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
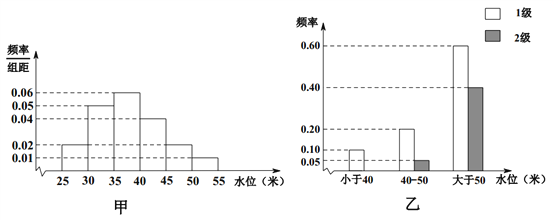
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各图中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB//平面MNP的图形的序号是( )
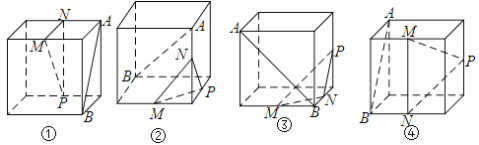
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .直线
.直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() .记点
.记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程.
的方程.
(Ⅱ)已知直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() ,轨迹
,轨迹![]() 在点
在点![]() 处的切线与线段
处的切线与线段![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com