Question

【题目】已知椭圆C1： =1（a＞b＞0）的离心率为e= ，且过点（1， ）．抛物线C2：x2=﹣2py（p＞0）的焦点坐标为（0，﹣ ）．
（Ⅰ）求椭圆C1和抛物线C2的方程；
（Ⅱ）若点M是直线l：2x﹣4y+3=0上的动点，过点M作抛物线C2的两条切线，切点分别为A，B，直线AB交椭圆C1于P，Q两点．
（i）求证直线AB过定点，并求出该定点坐标；
（ii）当△OPQ的面积取最大值时，求直线AB的方程．

Answer 1

【答案】解：（I）由于椭圆C1中， ，
则设其方程为 ，
由于点 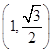在椭圆上，故代入得λ=1．
故椭圆C1的方程为 ．
抛物线C2中，
∵抛物线C2：x2=﹣2py（p＞0）的焦点坐标为（0，﹣ ），
∴ ，故p=1，
从而椭圆C1的方程为 ，抛物线C2的方程为x2=﹣2y．
（II）（i）证明：设点M（x0 ， y0），且满足2x0﹣4y0+3=0，
点A（x1 ， y1），B（x2 ， y2），则切线MA的斜率为﹣x1 ，
从而MA的方程为y=﹣x1（x﹣x1）+y1 ，
考虑到 ，则切线MA的方程为x1x+y+y1=0，
同理切线MB的方程为x2x+y+y2=0，
由于切线MA，MB同过点M，
从而有 ，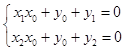
由此点A（x1 ， y1），B（x2 ， y2）在直线x0x+y+y0=0上．
又点M在直线2x﹣4y+3=0上，则2x0﹣4y0+3=0，
故直线AB的方程为（4y0﹣3）x+2y+2y0=0，
即y0（4x+2）+（2y﹣3x）=0，
∴直线AB过定点 ．
（ii）解：设P（x3 ， y3），Q（x4 ， y4），
考虑到直线AB的方程为x0x+y+y0=0，
则联立方程 ，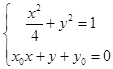
消去y并简化得 ，
从而 ， ， ，
从而 ，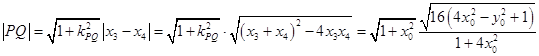
点O到PQ的距离 ，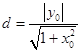
从而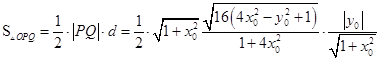
= ，
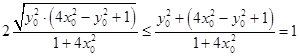当且仅当 ，即 ，
又由于2x0﹣4y0+3=0，
从而消去x0得 ，
即 ，解得 ，
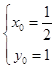从而 或 ，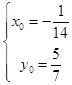
∴所求的直线为x+2y+2=0或x﹣14y﹣10=0
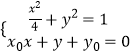【解析】（I）由已知条件，设椭圆方程为 ，把点 代入能求出椭圆C1的方程．抛物线C2中，由 ，能求出抛物线C2的方程．（II）（i）设点M（x0 ， y0），且满足2x0﹣4y0+3=0，点A（x1 ， y1），B（x2 ， y2），由于切线MA，MB同过点M，有 ，由此能证明直线AB过定点 ．（ii）设P（x3 ， y3），Q（x4 ， y4），联立方程 ，得 ，由此利用根的判别式和韦达定理能求出直线方程．