
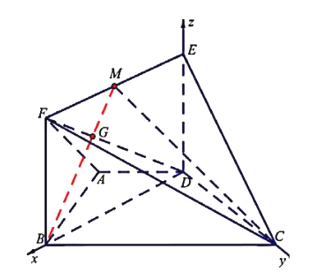
【题目】如图,已知四边形![]() 为直角梯形,
为直角梯形,![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() .
.
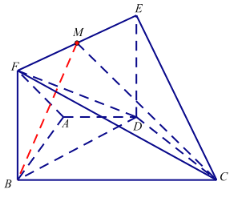
(1)若点![]() 为
为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(2)若点![]() 为线段
为线段![]() 上一动点,求
上一动点,求![]() 与平面
与平面![]() 所成角的取值范围.
所成角的取值范围.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)在直角梯形![]() 中根据长度关系和勾股定理,可证
中根据长度关系和勾股定理,可证![]() ,再由已知条件可得
,再由已知条件可得![]() 面
面![]() ,从而有
,从而有![]() ,在矩形
,在矩形![]() 中,可得
中,可得![]() ,可证出
,可证出![]() ,即证证明结论;
,即证证明结论;
(2)以![]() 为坐标原点建立空间直角坐标系,确定出
为坐标原点建立空间直角坐标系,确定出![]() 坐标,设
坐标,设![]() ,
,![]() ,求出平面
,求出平面![]() 的法向量,进而求出直线
的法向量,进而求出直线![]() 与平面
与平面![]() 所成角正弦的取值范围,即可求解.
所成角正弦的取值范围,即可求解.
(1)法一:在直角梯形![]() 中,
中,![]() ,
,
![]() ,故由勾股定理知
,故由勾股定理知![]() ,
,
取![]() 中点
中点![]() ,则
,则![]() 中,
中,
![]() ,又
,又![]()
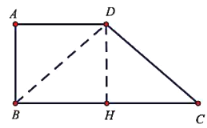
![]() 中,
中,![]() ,故
,故![]() .
.
因为平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,
所以![]() 面
面![]() .
.
![]() 面
面![]() ,故
,故![]() .
.
![]() 和
和![]() ,
,![]() ,
,
![]() ,故
,故![]() .
.
故![]() ,
,
即![]() ,即
,即![]() .
.
又![]() ,
,![]() 面
面![]() ,故
,故![]() 面
面![]() .
.
法二:
因为平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,
![]() 面
面![]() 且
且![]() .所以
.所以![]() 面
面![]() .
.
建立空间直角坐标系![]() 如图,则
如图,则
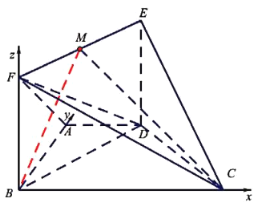
![]() .
.
![]() ,
,![]() ,
,![]() ,故
,故
![]() ,
,![]() .
.
![]() ,又
,又![]() ,
,
![]() 面
面![]() ,故
,故![]() 面
面![]() .
.
(2)法一:因为平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,
![]() 面
面![]() 且
且![]() .所以
.所以![]() 面
面![]() ,
,
建立空间直角坐标系![]() 如图,则
如图,则
![]() ,
,
设![]() ,则
,则![]()
则![]()
设平面![]() 的法向量为
的法向量为![]()
∴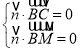 ,即
,即![]() ,故
,故![]() ,
,
取![]() ,则
,则![]() ,故
,故
平面![]() 的一个法向量为
的一个法向量为![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
∴![]()
∴当![]() 时取最大值
时取最大值![]() ,当
,当![]() 时取最小值
时取最小值![]()
故![]() 与平面
与平面![]() 所成角的取值范围为
所成角的取值范围为![]() .
.
法二:根据(1)知![]() ,
,![]() 面
面![]() .
.
建立空间直角坐标系![]() 如图,则
如图,则![]() ,
,
设![]() ,则
,则![]()
则![]()
设平面![]() 的法向量为
的法向量为![]()
∴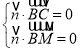 ,即
,即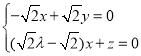 ,
,
故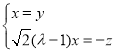 ,取
,取![]() ,则
,则![]() ,
,
故平面![]() 的一个法向量为
的一个法向量为
![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
∴![]()
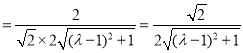 ,
,
∴当![]() 时取最大值
时取最大值![]() ,当
,当![]() 时取最小值
时取最小值![]()
故![]() 与平面
与平面![]() 所成角的取值范围为
所成角的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(.(12分)在一次购物抽奖活动中,假设某10张券中有一等奖奖券1张,可获价值50元的奖品;有二等奖奖券3张,每张可获价值10元的奖品;其余6张没奖。某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名运动员进行射击训练,已知他们击中的环数都稳定在![]() 、
、![]() 、
、![]() 、
、![]() 环,且每次射击成绩互不影响.根据以往的统计数据,甲、乙射击环数的频率分布条形图如下:
环,且每次射击成绩互不影响.根据以往的统计数据,甲、乙射击环数的频率分布条形图如下:
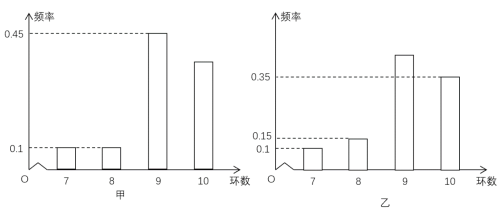
若将频率视为概率,回答下列问题:
(1)甲、乙各射击一次,求甲、乙同时击中![]() 环的概率;
环的概率;
(2)求甲射击一次,击中![]() 环以上(含
环以上(含![]() 环)的概率;
环)的概率;
(3)甲射击![]() 次,
次,![]() 表示这
表示这![]() 次射击中击中
次射击中击中![]() 环以上(含
环以上(含![]() 环)的次数,求
环)的次数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-x2+a,x∈R,曲线y=f(x)在(0,f(0))处的切线方程为y=bx.
(1)求f(x)的解析式;
(2)当x∈R时,求证:f(x)≥-x2+x;
(3)若f(x)≥kx对任意的x∈(0,+∞)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 个人排成一排,在下列情况下,各有多少种不同排法?
个人排成一排,在下列情况下,各有多少种不同排法?
(1)甲不在两端;
(2)甲、乙、丙三个必须在一起;
(3)甲、乙必须在一起,且甲、乙都不能与丙相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:
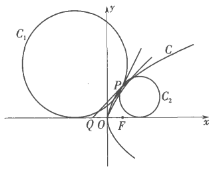
【题目】如图,在平面直角坐标系xOy中,F为x轴正半轴上的一个动点.以F为焦点、O为顶点作抛物线C.设P为第一象限内抛物线C上的一点,Q为x轴负半轴上一点,使得PQ为抛物线C的切线,且![]() .圆C1、C2均与直线OP切于点P,且均与x轴相切.求点F的坐标,使圆C1与C2的面积之和取到最小值,
.圆C1、C2均与直线OP切于点P,且均与x轴相切.求点F的坐标,使圆C1与C2的面积之和取到最小值,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com