


科目:高中数学 来源: 题型:
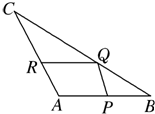 如图,△ABC是一块边长AB=3m,AC=5m,BC=7m的剩余角料.现要从中裁剪出一块面积最大的平行四边形用料APQR,要求顶点P,Q,R分别在边AB,BC,CA上.问点Q在BC边上的什么位置时,剪裁符合要求?并求这个最大值.
如图,△ABC是一块边长AB=3m,AC=5m,BC=7m的剩余角料.现要从中裁剪出一块面积最大的平行四边形用料APQR,要求顶点P,Q,R分别在边AB,BC,CA上.问点Q在BC边上的什么位置时,剪裁符合要求?并求这个最大值.查看答案和解析>>
科目:高中数学 来源: 题型:
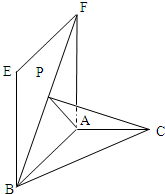
 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):查看答案和解析>>
科目:高中数学 来源: 题型:
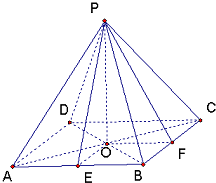
 (2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2
(2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2| 3 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修2) 2009-2010学年 第18期 总174期 人教课标高一版 题型:047
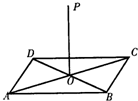
如图,P是平面四边形ABCD所在平面外一点,且AB=BC,AD=DC,PA=PC.
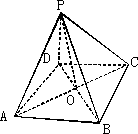
求证:平面PAC⊥平面PBD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com