解:(1)∵a
1=1,a
n+1=2a
n+2
n(n∈N
*),∴
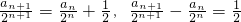
.…(3分)
∴

.…(5分)
∴a
n=n•2
n-1(n∈N
*).…(6分)
(2)设等差数列{b
n}的首项为b
1,公差为d,则b
n=b
1+(n-1)d(n∈N
*).…(7分)
考察等差数列,易知:b
1+b
n+1=b
2+b
n=b
3+b
n-1=…=b
n+1+b
1.
又 b
1C
n0+b
2C
n1+b
3C
n2+…+b
n+1C
nn=a
n+1,利用加法交换律把此等式变为b
n+1C
nn+b
nC
nn-1+b
n-1C
nn-2+…+b
1C
n0=a
n+1,
两式相加,利用组合数的性质C
nm=C
nn-m化简,得(b
1+b
n+1)(C
n0+C
n1+…+C
nn)=2a
n+1,即b
1+b
n+1=2n+2.…(10分)
再分别令n=1,n=2,得

,进一步可得
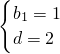
.…(11分)
因此,满足题设的等差数列{b
n}的通项公式为b
n=2n-1(n∈N
*).…(12分)
(3)结论:
存在正常数M(只要M>6即可)使得
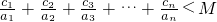
对n∈N
*恒成立.(13分)
证明 由(2)知,b
n=2n-1,于是,c
n=n(2n-1),
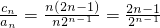
.…(14分)
记
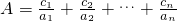
,则
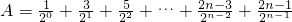
,

.此两式相差,得
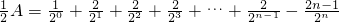
.进一步有
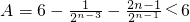
.…(18分)
所以,当且仅当正常数M>6时,
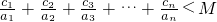
对n∈N
*恒成立.
分析:(1)根据数列递推式a
n+1=2a
n+2
n,可得
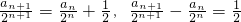
从而得证,进而可求数列的通项;
(2)设等差数列{b
n}的首项为b
1,公差为d,则b
n=b
1+(n-1)d(n∈N
*),从而有b
1+b
n+1=b
2+b
n=b
3+b
n-1=…=b
n+1+b
1.
条件 b
1C
n0+b
2C
n1+b
3C
n2+…+b
n+1C
nn=a
n+1,利用加法交换律把此等式变为b
n+1C
nn+b
nC
nn-1+b
n-1C
nn-2+…+b
1C
n0=a
n+1,
两式相加,利用组合数的性质C
nm=C
nn-m化简,即可求得满足题设的等差数列;
(3)可得结论存在正常数M(只要M>6即可)使得
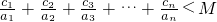
对n∈N
*恒成立,先表示出
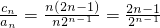
,进而利用错位相减法求和,从而可得结论.
点评:本题以数列递推式为载体,考查构造法证明等差数列,考查等差数列项的性质,考查错位相减法求和,综合性强.

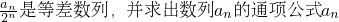 ;
;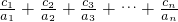 <M对n∈N*恒成立,并证明你的结论.
<M对n∈N*恒成立,并证明你的结论.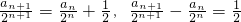 .…(3分)
.…(3分) .…(5分)
.…(5分) ,进一步可得
,进一步可得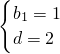 .…(11分)
.…(11分)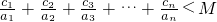 对n∈N*恒成立.(13分)
对n∈N*恒成立.(13分)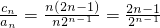 .…(14分)
.…(14分)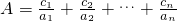 ,则
,则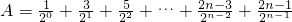 ,
, .此两式相差,得
.此两式相差,得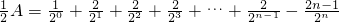 .进一步有
.进一步有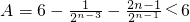 .…(18分)
.…(18分)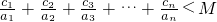 对n∈N*恒成立.
对n∈N*恒成立.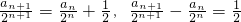 从而得证,进而可求数列的通项;
从而得证,进而可求数列的通项;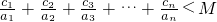 对n∈N*恒成立,先表示出
对n∈N*恒成立,先表示出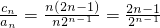 ,进而利用错位相减法求和,从而可得结论.
,进而利用错位相减法求和,从而可得结论.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案