
【题目】作为交通重要参与者的行人,闯红灯通行频有发生,带来了较大的交通安全隐患.在某十字路口,交警部门从穿越该路口的行人中随机抽取了200人进行调查,得到不完整的![]() 列联表如图所示:
列联表如图所示:
年龄低于30岁 | 年龄不低于30岁 | 合计 | |
闯红灯 | 60 | 80 | |
未闯红灯 | 80 | ||
合计 | 200 |
(1)将![]() 列联表补充完整;
列联表补充完整;
(2)是否有99.9%的把握认为行人是否闯红灯与年龄有关.
参考公式及数据: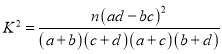 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() 且过点
且过点![]() 椭圆C与
椭圆C与![]() 轴的交点为A、B(点A位于点B的上方),直线
轴的交点为A、B(点A位于点B的上方),直线![]() 与椭圆C交于不同的两点M、N(点M位于点N的上方).
与椭圆C交于不同的两点M、N(点M位于点N的上方).

(1)求椭圆C的方程;
(2)求△OMN面积的最大值;
(3)求证:直线AN和直线BM交点的纵坐标为常值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(4,0)、B(1,0),动点M满足|AM|=2|BM|.
(1)求动点M的轨迹C的方程;
(2)直线l:x+y=4,点N∈l,过N作轨迹C的切线,切点为T,求NT取最小时的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P到定点![]() 的距离与点P到定直线
的距离与点P到定直线![]() 的距离之比为
的距离之比为![]()
(1)求动点P的轨迹C的方程;
(2)设M、N是直线l上的两个点,点E是点F关于原点的对称点,若![]() ,求 | MN | 的最小值.
,求 | MN | 的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当函数的自变量取值区间与值域区间相同时,我们称这样的区间为该函数的保值区间,函数的保值区间有![]() 、
、![]() 、
、![]() 三种形式,以下四个二次函数图像的对称轴是直线
三种形式,以下四个二次函数图像的对称轴是直线![]() ,从图像可知,有二个保值区间的函数是( )
,从图像可知,有二个保值区间的函数是( )
A.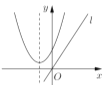 B.
B. C.
C.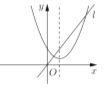 D.
D.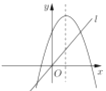
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等边![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且满足
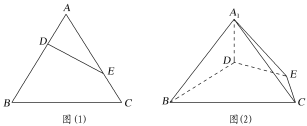
上的点,且满足![]() (如图(1)),将
(如图(1)),将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连接
成直二面角,连接![]() ,
,![]() (如图(2)).
(如图(2)).
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com