
【题目】设函数![]() .
.
(1)求该函数的单调区间;
(2)若当x∈[﹣2,2]时,不等式f(x)<m恒成立,求实数m的取值范围.
【答案】(1)单调递增区间为(﹣∞,﹣2),(0,+∞),单调减区间为(﹣2,0);
(2)m>2e2.
【解析】
(1)求出导函数f′(x),令导函数f′(x)>0,求解即可求得单调增区间,令f′(x)<0,求解即可求得单调减区间,从而求得答案;
(2)将恒成立问题转化成求函数f(x)最大值,利用导数求出函数f(x)的最大值,即可求得实数m的取值范围.
(1)∵![]() ,
,
∴f′(x)=xex![]() x2ex
x2ex![]() exx(x+2),
exx(x+2),
令f′(x)>0,解得x>0或x<﹣2,
令f′(x)<0,解得﹣2<x<0,
∴f(x)的单调递增区间为(﹣∞,﹣2),(0,+∞),单调减区间为(﹣2,0);
(2)∵当x∈[﹣2,2]时,不等式f(x)<m恒成立,
∴m>f(x)max,
由(1)可知,f′(x)=xex![]() x2ex
x2ex![]() exx(x+2),
exx(x+2),
令f′(x)=0,可得x=﹣2或x=0,
∵f(﹣2)![]() ,f(0)=0,f(2)=2e2,
,f(0)=0,f(2)=2e2,
∴f(x)max=2e2,
∴m>2e2,
∴实数m的取值范围为m>2e2.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
B. 命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
C. 命题“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,都有
,都有![]() ”
”
D. 若![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的30个零件编号为01,02,…,19,30,现利用如下随机数表从中抽取5个进行检测. 若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件编号为( )
34 57 07 86 36 04 68 96 08 23 23 45 78 89 07 84 42 12 53 31 25 30 07 32 86 |
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高一年级学生的智力水平,某校按1:10的比例对700名高一学生按性别分别进行“智力评分”抽样调查,测得“智力评分”的频数分布表如表1、表2所示.
表1:男生“智力评分”频数分布表
智力评分/分 |
|
|
|
|
|
|
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生“智力评分”频数分布表
智力评分/分 |
|
|
|
|
|
|
频数 | 1 | 7 | 12 | 6 | 3 | 1 |

(1)求高一年级的男生人数,并完成下面男生“智力评分”的频率分布直方图;
(2)估计该校高一年级学生“智力评分”在![]() 内的人数.
内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解中学生对交通安全知识的掌握情况,从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
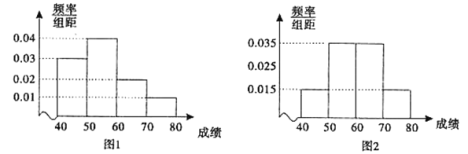
(Ⅰ)分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩;
(Ⅱ)完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
农村中学 | |||
城镇中学 | |||
合计 |
附:![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋内有3个不同的红球,4个不同的白球
(1)从中任取3个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不少于6分的取法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(请写出式子在写计算结果)有4个不同的小球,4个不同的盒子,现在要把球全部放入盒内:
(1)共有多少种方法?
(2)若每个盒子不空,共有多少种不同的方法?
(3)恰有一个盒子不放球,共有多少种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l的极坐标方程为θ=α(ρ∈R,ρ≠0),其中α∈[0,π),曲线C1的参数方程为![]() (t为参数),圆C2的普通方程为x2+y2+2
(t为参数),圆C2的普通方程为x2+y2+2![]() x=0.
x=0.
(1)求C1,C2的极坐标方程;
(2)若l与C1交于点A,l与C2交于点B,当|AB|=2时,求△ABC2的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com