解:(I)证明:因为f′(x)=

+x
2且0≤x

所以f′(x)=

+x
2∴f′(x)∈[

,1)满足条件0<f′(x)<1
又因为当x=0时,飞(0)-0=0,所以方程飞(x)-x=0有实数根0.
所以函数f(x)=

+

(0≤x<

)是集合M中的元素
(II)证明:∵f(n)-f(m)=

∴


∵[m,n]⊆[0,

)∴
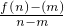
=

∈(

+m
2,

+n
2).
又∵f′(x)=

+x
2,
∴当0≤m<x<n<

时,f′(x)∈(

+m
2,

+n
2).
∴存在x
0∈(m,n)使得
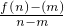
=f′(x
0)也就是f(n)-(m)=(n-m)f′(x
0);
(III)假设方程f(x)-x=0存在两个实数根α,β(α≠β),则f(α)-α=0,f(β)-β=0不妨设α<β,根据题意存在数c∈(α,β)
使得等式f(β)-f(α)=(β-α)f′(c)成立.
因为f(α)=α,f(β)=β且α≠β,所以f′(c)=1
与已知0<f′(x)<1矛盾,所以方程f(x)-x=0只有一个实数根.…(14分)
分析:(I)根据所给的条件得到f′(x)∈[

,1)满足条件0<f′(x)<1又因为当x=0时,飞(0)-0=0,所以方程飞(x)-x=0有实数根0.得到结论.
(II)要证等式f(n)-f(m)=(n-m)f′(x
o)成立,先整理出f(n)-f(m),再做出和n-m的比值,根据等于的函数式整理出存在x
o∈(m,n),使得等式f(n)-f(m)=(n-m)f′(x
o)成立.
(III)先假设方程有两个实根,根据题意 存在c使得f(n)-f(m)=(n-m)f′(x
o)成立,得到矛盾,最后得到所给的方程只有一个实根.
点评:本题考查函数恒成立问题,本题的题干比较长,解题的关键是读懂题目,题目的运算量不大,只要理解题意这只是一道中档题目,也可以作为一套试卷中的压轴题目出现.

 +
+ (0≤x<
(0≤x< )是集合M中的元素;
)是集合M中的元素; +
+ (0≤x
(0≤x )具有下面的性质:对于任意[m,n]⊆[0,
)具有下面的性质:对于任意[m,n]⊆[0, ),都存在xo∈(m,n),使得等式f(n)-f(m)=(n-m)f′(xo)成立.
),都存在xo∈(m,n),使得等式f(n)-f(m)=(n-m)f′(xo)成立. +x2且0≤x
+x2且0≤x 所以f′(x)=
所以f′(x)= +x2
+x2 ,1)满足条件0<f′(x)<1
,1)满足条件0<f′(x)<1 +
+ (0≤x<
(0≤x< )是集合M中的元素
)是集合M中的元素


 )∴
)∴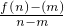 =
= ∈(
∈( +m2,
+m2, +n2).
+n2). +x2,
+x2, 时,f′(x)∈(
时,f′(x)∈( +m2,
+m2, +n2).
+n2).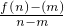 =f′(x0)也就是f(n)-(m)=(n-m)f′(x0);
=f′(x0)也就是f(n)-(m)=(n-m)f′(x0); ,1)满足条件0<f′(x)<1又因为当x=0时,飞(0)-0=0,所以方程飞(x)-x=0有实数根0.得到结论.
,1)满足条件0<f′(x)<1又因为当x=0时,飞(0)-0=0,所以方程飞(x)-x=0有实数根0.得到结论.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案