
【题目】若一个人从出生到死亡,在每个生日都测量身高,并作出这些数据的散点图,这些点将不会落在一条直线上,但在一段时间内的增长数据有时可以用线性回归来分析,下表是一位母亲给儿子做的成长记录:
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
(1)年龄(解释变量)和身高(预报变量)之间具有怎样的相关关系?
(2)如果年龄相差5岁,则身高有多大差异(3~16岁之间)?
(3)如果身高相差20 cm,其年龄相差多少(3~16岁之间)?
(4)试判断该函数模型是否能够较好地反映年龄与身高的关系.
【答案】(1)答案见解析;(2)![]() ;(3)3岁;(4)答案见解析
;(3)3岁;(4)答案见解析
【解析】
解:(1)设年龄x与身高y之间的回归直线方程为![]() =
=![]() x+
x+![]() ,由公式
,由公式![]() =
=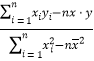 得
得![]() ≈6.286,
≈6.286,![]() =
=![]() -
-![]()
![]() ≈72,所以
≈72,所以![]() =6.286x+72.
=6.286x+72.
(2)如果年龄相差5岁,则预报变量变化6.286×5=31.425,即身高相差约31.4 cm.
(3)如果身高相差20 cm,年龄相差Δx=![]() =3.182≈3(岁).
=3.182≈3(岁).
(4)
y | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| 90.9 | 97.1 | 103.4 | 109.7 | 116.0 | 122.3 | 128.6 |
y | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
| 134.9 | 141.1 | 147.4 | 153.7 | 160.0 | 166.3 | 172.6 |
由表得R2=1-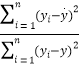 ≈0.999 7.由R2=0.999 7,表明年龄解释了99.97%的身高的变化,拟合效果较好.
≈0.999 7.由R2=0.999 7,表明年龄解释了99.97%的身高的变化,拟合效果较好.


科目:高中数学 来源: 题型:
【题目】已知曲线![]()
(1)若![]() ,求经过点
,求经过点![]() 且与曲线
且与曲线![]() 只有一个公共点的直线方程:
只有一个公共点的直线方程:
(2)若![]() ,请在直角坐标平面内找出纵坐标不同的两个点,此两点满足条件:无论
,请在直角坐标平面内找出纵坐标不同的两个点,此两点满足条件:无论![]() 如何变化,这两个点都不在曲线
如何变化,这两个点都不在曲线![]() 上;
上;
(3)若曲线![]() 与线段
与线段![]() 有公共点,求
有公共点,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+ ![]() )(ω>0)的最小正周期为π,则该函数的图象( )
)(ω>0)的最小正周期为π,则该函数的图象( )
A.关于直线x= ![]() 对称
对称
B.关于点( ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网上购物系统是一种具有交互功能的商业信息系统,它在网络上建立一个虚拟的购物商场,使购物过程变得轻松、快捷、方便.网上购物系统分为前台管理和后台管理,前台管理包括浏览商品、查询商品、订购商品、用户注册等功能;后台管理包括公告管理、商品管理、订单管理、投诉管理和用户管理等模块.根据这些要求画出该系统的结构图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冶炼某种金属可以用旧设备和改造后的新设备,为了检验用这两种设备生产的产品中所含杂质的关系,调查结果如下表所示:
分类 | 杂质高 | 杂质低 |
旧设备 | 37 | 121 |
新设备 | 22 | 202 |
根据以上数据,则( )
A. 含杂质的高低与设备改造有关
B. 含杂质的高低与设备改造无关
C. 设备是否改造决定含杂质的高低
D. 以上答案都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=2acosθ(a≠0),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为 ![]() (t为参数).
(t为参数).
(1)求圆C的直角坐标方程(化为标准方程)和直线l的极坐标方程;
(2)若直线l与圆C只有一个公共点,且a<1,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,且AB=AD,BC=DC.
(1)求证:![]() ∥平面EFGH;
∥平面EFGH;
(2)求证:四边形EFGH是矩形.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是直角△ABC斜边BC上一点,AC= ![]() DC.
DC.
(I)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD=2 ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两个投资项目的利润率分别为随机变量X1和X2,根据市场分析,X1和X2的分布列分别为
X1 | 5% | 10% |
P | 0.8 | 0.2 |
X2 | 2% | 8% | 12% |
P | 0.2 | 0.5 | 0.3 |
(1)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差V(Y1)、V(Y2);
(2)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com