
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 边的中点,现把
边的中点,现把![]() 沿
沿![]() 折叠,使其与
折叠,使其与![]() 构成如图2所示的三棱锥
构成如图2所示的三棱锥![]() ,且
,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 夹角的余弦值.
夹角的余弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)在图1中,取CP的中点O,连接AO交CB于E,得AO⊥CP,在△OCB中,有AO⊥OB,即AO⊥平面PCB,
可证平面ACP⊥平面CPB.
(2)因为AO⊥平面CPB,且OC⊥OE,故可如图建立空间直角坐标系,则![]() ,
, ![]() ,求出平面的法向量,利用向量夹角公式即可求解.
,求出平面的法向量,利用向量夹角公式即可求解.
试题解析:
(1)如图1,取![]() 得中点
得中点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,
在![]() 中,因为
中,因为![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 边的中点,
边的中点,
所以![]() 是正三角形,所以
是正三角形,所以![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.
由折叠过程可知,在图2中, ![]() ,
, ![]() ,如图2,连接
,如图2,连接![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
所以![]() ,所以
,所以![]() .又因为
.又因为![]() ,
, ![]() ,
,
所以![]() ,又因为
,又因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
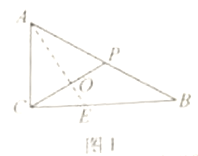
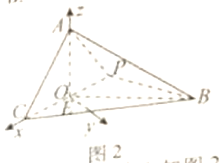
(2)因为![]() 平面
平面![]() ,且
,且![]() ,所以可建立如图二所示的空间直角坐标系.则
,所以可建立如图二所示的空间直角坐标系.则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
由![]() 得
得![]() .
.
同理可求得平面![]() 的一个法向量为
的一个法向量为![]() .
.
设所求角为![]() ,则所求角的余弦值
,则所求角的余弦值![]() .
.


科目:高中数学 来源: 题型:
【题目】现从某学校高一年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分成6组:第1组
之间,将测量结果按如下方式分成6组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
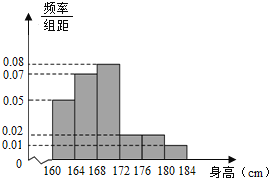
(1)求这50名男生身高的中位数,并估计该校高一全体男生的平均身高;
(2)求这50名男生当中身高不低于176![]() 的人数,并且在这50名身高不低于176
的人数,并且在这50名身高不低于176![]() 的男生中任意抽取2人,求这2人身高都低于180
的男生中任意抽取2人,求这2人身高都低于180![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月12时的气温状况,随机选取该月中的5天,将这5天中12时的气温数据(单位:![]() )制成如图所示的茎叶图.考虑以下结论:
)制成如图所示的茎叶图.考虑以下结论:
①甲地的平均气温低于乙地的平均气温;
②甲地的平均气温高于乙地的平均气温;
③甲地气温的标准差小于乙地气温的标准差;
④甲地气温的标准差大于乙地气温的标准差.
其中根据茎叶图能得到的统计结论的标号为( )
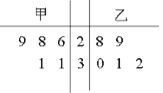
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点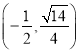 ,且离心率为
,且离心率为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 的右顶点,探究:
的右顶点,探究: ![]() 是否为定值,若是,求出该定值,若不是,请说明理由.(其中,
是否为定值,若是,求出该定值,若不是,请说明理由.(其中, ![]() ,
, ![]() 分别是直线
分别是直线![]() 、
、![]() 的斜率)
的斜率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们常这样说:“如果你的物理成绩好,那么你的数学学习就不会有什么大问题.”某班针对“高中物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系,如表为该班随机抽取6名学生在一次考试中的物理和数学成绩:
学生编号 学科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成绩(x) | 75 | 65 | 75 | 65 | 60 | 80 |
数学成绩(y) | 125 | 117 | 110 | 103 | 95 | 110 |
(1)求数学成绩y对物理成绩x的线性回归方程;
(2)该班某同学的物理成绩100分,预测他的数学成绩.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
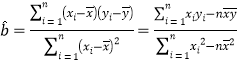 ,
,![]()
参考数据:752+652+752+652+602+802=29700,
75×125+65×117+75×110+65×103+60×95+80×110=46425.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经济开发区规划要修建一地下停车场,停车场横截面是如图所示半椭圆形AMB,其中AP为2百米,BP为4百米,![]() ,M为半椭圆上异于A,B的一动点,且
,M为半椭圆上异于A,B的一动点,且![]() 面积最大值为
面积最大值为![]() 平方百米,如图建系.
平方百米,如图建系.
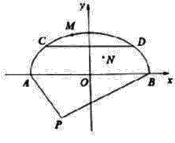
![]() 求出半椭圆弧的方程;
求出半椭圆弧的方程;
![]() 若要将修建地下停车场挖出的土运到指定位置P处,N为运土点,以A,B为出口,要使运土最省工,工程部需要指定一条分界线,请求出分界线所在的曲线方程;
若要将修建地下停车场挖出的土运到指定位置P处,N为运土点,以A,B为出口,要使运土最省工,工程部需要指定一条分界线,请求出分界线所在的曲线方程;
![]() 若在半椭圆形停车场的上方修建矩形商场,矩形的一边CD与AB平行,设
若在半椭圆形停车场的上方修建矩形商场,矩形的一边CD与AB平行,设![]() 百米,试确定t的值,使商场地面的面积最大.
百米,试确定t的值,使商场地面的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了了解职工的工作状况,随机抽取了一个车间对职工工作时间的情况进行暗访,工作时间在![]() 小时及以上的为合格.把所得数据进行整理后,分成
小时及以上的为合格.把所得数据进行整理后,分成![]() 组画出频率分布直方图(如图所示),但由于工作疏忽,没有画出最后一组,只知道最后一组的频数是
组画出频率分布直方图(如图所示),但由于工作疏忽,没有画出最后一组,只知道最后一组的频数是![]() .
.
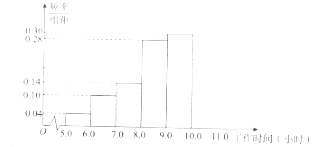
(Ⅰ)求这次暗访中工作时间不合格的人数;
(Ⅱ)已知在工作时间超过![]() 小时的人中有两名女职工,现要从工作时间在
小时的人中有两名女职工,现要从工作时间在![]() 小时以上的人中选出两名代表在职工代表大会上发言,求至少选出一位女职工作代表的概率.
小时以上的人中选出两名代表在职工代表大会上发言,求至少选出一位女职工作代表的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com