
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(2,﹣2).
=(2,﹣2).
(1)设 ![]() =4
=4 ![]() +
+ ![]() ,求
,求 ![]() ;
;
(2)若 ![]() +
+ ![]() 与
与 ![]() 垂直,求λ的值;
垂直,求λ的值;
(3)求向量 ![]() 在
在 ![]() 方向上的投影.
方向上的投影.
【答案】
(1)解:∵向量 ![]() =(1,2),
=(1,2), ![]() =(2,﹣2).
=(2,﹣2).
∴ ![]() =4
=4 ![]() +
+ ![]() =(6,6),
=(6,6),
∴ ![]() =2×6﹣2×6=0
=2×6﹣2×6=0
∴ ![]()
(2)解: ![]() +λ
+λ ![]() =(1,2)+λ(2,﹣2)=(2λ+1,2﹣2λ),
=(1,2)+λ(2,﹣2)=(2λ+1,2﹣2λ),
由于 ![]() +λ
+λ ![]() 与
与 ![]() 垂直,
垂直,
∴2λ+1+2(2﹣2λ)=0,
∴λ= ![]() .
.
(3)解:设向量 ![]() 与
与 ![]() 的夹角为θ,
的夹角为θ,
向量 ![]() 在
在 ![]() 方向上的投影为|
方向上的投影为| ![]() |cos θ.
|cos θ.
∴| ![]() |cos θ=
|cos θ= ![]() =
= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]()
【解析】(1)由已知中向量 ![]() =(1,2),
=(1,2), ![]() =(2,﹣2),
=(2,﹣2), ![]() =4
=4 ![]() +
+ ![]() ,可得向量
,可得向量 ![]() 的坐标,代入向量数量积公式可得
的坐标,代入向量数量积公式可得 ![]() 的值,再代入数乘向量公式,可得答案.(2)若
的值,再代入数乘向量公式,可得答案.(2)若 ![]() +
+ ![]() 与
与 ![]() 垂直,则(
垂直,则( ![]() +
+ ![]() )
) ![]() =0垂直,进而可构造关于λ的方程,解方程可得λ的值.(3)根据向量
=0垂直,进而可构造关于λ的方程,解方程可得λ的值.(3)根据向量 ![]() 在
在 ![]() 方向上的投影为|
方向上的投影为| ![]() |cos θ=
|cos θ= ![]() ,代入可得答案.
,代入可得答案.
【考点精析】利用数量积判断两个平面向量的垂直关系对题目进行判断即可得到答案,需要熟知若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直.
两平面的法向量垂直.


科目:高中数学 来源: 题型:
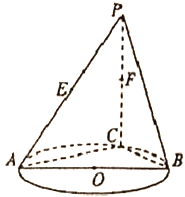
【题目】如图, ![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 、
、![]() 的点,直线度
的点,直线度![]() 平面
平面![]() ,
, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(Ⅰ)设平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(Ⅱ)设(Ⅰ)中的直线![]() 与圆
与圆![]() 的另一个交点为点
的另一个交点为点![]() ,且满足
,且满足![]() ,
, ![]() ,当二面角
,当二面角![]() 的余弦值为
的余弦值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A、B、C三点满足 ![]() =
= ![]() +
+ ![]() .
.
(1)求证:A、B、C三点共线;
(2)已知A(1,cosx)、B(1+sinx,cosx),x∈[0, ![]() ],f(x)=
],f(x)= ![]()
![]() +(2m+
+(2m+ ![]() )|
)| ![]() |+m2的最小值为5,求实数m的值.
|+m2的最小值为5,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c.
(1)若f(﹣1)=0,试判断函数f(x)零点个数;
(2)若对x1x2∈R,且x1<x2 , f(x1)≠f(x2),证明方程f(x)= ![]() 必有一个实数根属于(x1 , x2).
必有一个实数根属于(x1 , x2).
(3)是否存在a,b,c∈R,使f(x)同时满足以下条件
①当x=﹣1时,函数f(x)有最小值0;
②对任意x∈R,都有0≤f(x)﹣x≤ ![]() 若存在,求出a,b,c的值,若不存在,请说明理由.
若存在,求出a,b,c的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与
与![]() (
(![]() 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为![]() .若动点
.若动点![]() 满足
满足![]() ,试探究是否存在两个定点
,试探究是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如下图所示(![]() (吨)为买进蔬菜的质量,
(吨)为买进蔬菜的质量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;

(Ⅱ)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店准备一次性买进25吨,则预计需要销售多少天.
参考公式:  ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com