
【题目】已知![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() (
(![]() ).
).
(1)求函数![]() 的解析式;
的解析式;
(2)求函数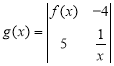 在
在![]() 条件下的最小值;
条件下的最小值;
(3)把![]() 的图像按向量
的图像按向量![]() 平移得到曲线
平移得到曲线![]() ,过坐标原点
,过坐标原点![]() 作
作![]() 、
、![]() 分别交曲线
分别交曲线![]() 于点
于点![]() 、
、![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 为锐角时,求
为锐角时,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() , O为DE的中点,
, O为DE的中点,![]() .F为
.F为![]() 的中点,平面
的中点,平面![]() 平面BCED.
平面BCED.
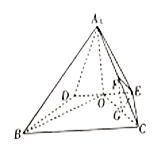
(1)求证:平面 ![]() 平面
平面![]() .
.
(2)线段OC上是否存在点G,使得![]() 平面EFG?说明理由。
平面EFG?说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司全年的纯利润为![]() 元,其中一部分作为奖金发给
元,其中一部分作为奖金发给![]() 位职工,奖金分配方案如下首先将职工工作业绩(工作业绩均不相同)从大到小,由1到
位职工,奖金分配方案如下首先将职工工作业绩(工作业绩均不相同)从大到小,由1到![]() 排序,第1位职工得奖金
排序,第1位职工得奖金![]() 元,然后再将余额除以
元,然后再将余额除以![]() 发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
(1)设![]() 为第
为第![]() 位职工所得奖金额,试求
位职工所得奖金额,试求![]() 并用
并用![]() 和
和![]() 表示
表示![]() (不必证明);
(不必证明);
(2)证明![]() 并解释此不等式关于分配原则的实际意义;
并解释此不等式关于分配原则的实际意义;
(3)发展基金与![]() 和
和![]() 有关,记为
有关,记为![]() 对常数
对常数![]() ,当
,当![]() 变化时,求
变化时,求![]() .(可用公式
.(可用公式![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,
,![]() ,
,![]() ,
,![]() 是椭圆上任意三点,
是椭圆上任意三点,![]() ,
,![]() 关于原点对称且满足
关于原点对称且满足![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)若斜率为![]() 的直线与圆:
的直线与圆:![]() 相切,与椭圆
相切,与椭圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() ,求
,求![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解![]() 地区足球特色学校的发展状况,某调查机构得到如下统计数据:
地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(Ⅰ)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(Ⅱ)求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 地区2019年足球特色学校的个数(精确到个)
地区2019年足球特色学校的个数(精确到个)
参考公式: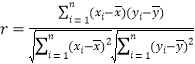 ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,定义函数
,定义函数![]() 对于两个集合
对于两个集合![]() ,定义集合
,定义集合![]() . 已知
. 已知![]() ,
, ![]() .
.
(Ⅰ)写出![]() 和
和![]() 的值,并用列举法写出集合
的值,并用列举法写出集合![]() ;
;
(Ⅱ)用![]() 表示有限集合
表示有限集合![]() 所含元素的个数,求
所含元素的个数,求![]() 的最小值;
的最小值;
(Ⅲ)有多少个集合对![]() ,满足
,满足![]() ,且
,且![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
![]() 1
1![]() 当
当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
![]() 2
2![]() 若
若![]() 是R上的单调递增函数,求a的取值范围;
是R上的单调递增函数,求a的取值范围;
![]() 3
3![]() 若函数
若函数![]() 对任意的实数
对任意的实数![]() ,存在唯一的实数
,存在唯一的实数![]() ,使得
,使得![]() 成立,求a的值.
成立,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2-x+16a)的定义域为R;命题q:不等式3x-9x<a对任意x∈R恒成立.
(1)如果p是真命题,求实数a的取值范围;
(2)如果命题“p或q”为真命题且“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com