已知集合A={x|x2+2x-3<0},B={x|y=lg(x+2)(3-x)}.
(Ⅰ)从A∪B中任取两个不同的整数,记事件E={两个不同的整数中至少有一个是集合A∩B中的元素},求P(E);
(Ⅱ)从A中任取一个实数x,从B中任取一个实数y,记事件F={x与y之差的绝对值不超过1},求P(F).
解:(Ⅰ)由已知可得:A={x|-3<x<1},B={x|-2<x<3},
∴A∪B={x|-3<x<3},A∩B={x|-2<x<1}
∵A∪B中的整数为-2,-1,0,1,2,
∴从中任取两个的所有可能情况为{-2,-1},{-2,0},{-2,1},{-2,2},{-1,0},{-1,1},{-1,2},{0,1},{0,2},{1,2}共10种,…(3分)

∵A∩B中的整数为-1,0,
∴事件E包含的基本事件为{-2,-1},{1,-1},{2,-1},{-2,0},{1,0},{2,0},{0,-1}共7个,…(5分)
∴

…(6分)
(Ⅱ)(x,y)可看成平面上的点,全部结果构成的区域为Ω={(x,y)|-3<x<1,-2<y<3},其面积为
S
Ω=4×5=20,…(8分)
事件F构成的区域为F={(x,y)|-3<x<1,-2<y<3,|x-y|≤1},
其为图中阴影部分,它的面积为

…(11分)
∴
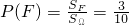
…(12分)
分析:(Ⅰ)由题意可得:A∪B中的整数为-2,-1,0,1,2,A∩B中的整数为-1,0,可列举得到方法种数,进而可得所要求的概率;
(Ⅱ)首先确定为几何概型,然后分别求两个面积可得答案.
点评:本题考查古典型和几何概型,分清两种概型是解决问题的关键,属基础题.

 ∵A∩B中的整数为-1,0,
∵A∩B中的整数为-1,0, …(6分)
…(6分) …(11分)
…(11分)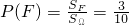 …(12分)
…(12分)
