
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:(1)若
是三个不同的平面,给出下列四个命题:(1)若![]() ,
,![]() ,则
,则![]() ;(2)若
;(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() ;(3)若
;(3)若![]() ,
,![]() ,则
,则![]() ;(4)若
;(4)若![]() ,
,![]() ,则
,则![]() ,其中正确命题的序号是( )
,其中正确命题的序号是( )
A.(1)(2)B.(2)(3)
C.(3)(4)D.(1)(4)
【答案】A
【解析】
根据线面平行性质定理,结合线面垂直的定义,可得①是真命题;根据面面平行的性质,结合线面垂直的性质,可得②是真命题;在正方体中举出反例,可得平行于同一个平面的两条直线不一定平行,垂直于同一个平面和两个平面也不一定平行,可得③④不正确,从而求解
对于①,因为![]() ,所以经过n作平面
,所以经过n作平面![]() ,使
,使![]() ,可得
,可得![]() ,又因为
,又因为![]() ,
,![]() ,所以
,所以![]() ,结合
,结合![]() 得
得![]() ,由此可得①是真命题;
,由此可得①是真命题;
对于②,因为![]() 且
且![]() ,所以
,所以![]() ,结合
,结合![]() ,可得
,可得![]() ,故②是真命题;
,故②是真命题;
对于③,设直线m、n是位于正方体上底面所在平面内的相交直线,而平面![]() 是正方体下底面所在的平面,则有
是正方体下底面所在的平面,则有![]() 且
且![]() 成立,但不能推出
成立,但不能推出![]() ,故③不正确;
,故③不正确;
对于④,设平面![]() 、
、![]() 、
、![]() 是位于正方体经过同一个顶点的三个面,则有
是位于正方体经过同一个顶点的三个面,则有![]() 且
且![]() ,但是
,但是![]() ,推不出
,推不出![]() ,故④不正确
,故④不正确
综上所述,其中正确命题的序号是①和②
故选:A


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设数集![]() 由实数构成,且满足:若
由实数构成,且满足:若![]() (
(![]() 且
且![]() ),则
),则![]() .
.
(1)若![]() ,试证明
,试证明![]() 中还有另外两个元素;
中还有另外两个元素;
(2)集合![]() 是否为双元素集合,并说明理由;
是否为双元素集合,并说明理由;
(3)若![]() 中元素个数不超过8个,所有元素的和为
中元素个数不超过8个,所有元素的和为![]() ,且
,且![]() 中有一个元素的平方等于所有元素的积,求集合
中有一个元素的平方等于所有元素的积,求集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1是某条公共汽车线路收支差额![]() 与乘客量的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象判断下列说法正确的是( )
与乘客量的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象判断下列说法正确的是( )
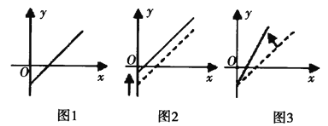
①图2的建议为减少运营成本;②图2的建议可能是提高票价;
③图3的建议为减少运营成本;④图3的建议可能是提高票价.
A.①④B.②④C.①③D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设国家收购某种农产品的价格是1.2元/kg,其中征税标准为每100元征8元(即税率为8个百分点,8%),计划可收购![]() kg.为了减轻农民负担,决定税率降低
kg.为了减轻农民负担,决定税率降低![]() 个百分点,预计收购可增加
个百分点,预计收购可增加![]() 个百分点.
个百分点.
(1)写出税收![]() (元)与
(元)与![]() 的函数关系;
的函数关系;
(2)要使此项税收在税率调节后不低于原计划的78%,确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入3×3的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么不同的三阶幻方的个数是( )
4 | 9 | 2 |
3 | 5 | 7 |
8 | 1 | 6 |
A.9B.8C.6D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点E,F,G分别为棱AB,
,点E,F,G分别为棱AB,![]() ,
,![]() 的中点,下列结论中,正确结论的序号是___________.
的中点,下列结论中,正确结论的序号是___________.
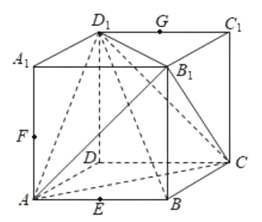
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④异面直线EF与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(3+x)+lg(3-x).
(1)判断![]() 的奇偶性并加以证明;
的奇偶性并加以证明;
(2)判断![]() 的单调性(不需要证明);
的单调性(不需要证明);
(3)解关于m的不等式f( m )- f( m+1)﹤0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆上.
在椭圆上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设动直线
)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() ,
, ![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 、
、![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com