
【题目】三角形![]() 中,边
中,边![]() 和
和![]() 所在的直线方程分别为
所在的直线方程分别为![]() 和
和![]() ,
,![]() 的中点为
的中点为![]() .
.
(1)求![]() 的坐标;
的坐标;
(2)求角![]() 的内角平分线所在直线的方程.
的内角平分线所在直线的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据边![]() 和
和![]() 所在的直线方程联立求解可得A,设
所在的直线方程联立求解可得A,设![]() ,由
,由![]() 的中点为
的中点为![]() ,列出方程解得B、C;
,列出方程解得B、C;
(2)由(1)得出BC直线方程为3x+y-10=0,设角![]() 的内角平分线所在直线的上的点为P(x,y),根据角平分线性质,则P点到AB、BC的距离相等,由距离公式可解出P点轨迹方程即为所求.
的内角平分线所在直线的上的点为P(x,y),根据角平分线性质,则P点到AB、BC的距离相等,由距离公式可解出P点轨迹方程即为所求.
(1)边![]() 和
和![]() 所在的直线方程分别为
所在的直线方程分别为![]() 和
和![]() ,
,
∴两直线方程联立解得![]() ,
,
∴点![]() ,
,
∵![]() 的中点为
的中点为![]() ,设
,设![]() ,
,
∴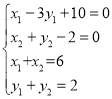 ,解得
,解得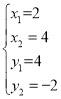 ,
,
即![]() ,
,
(2)BC直线方程为3x+y-10=0,
设角![]() 的内角平分线所在直线的上的点为P(x,y),
的内角平分线所在直线的上的点为P(x,y),
根据角平分线性质,P点到AB、BC的距离相等,
可得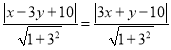 ,
,
化简可得![]() 或者
或者![]() ,
,
根据三角形![]() 在坐标系中位置,
在坐标系中位置,
可得角B内角平分线所在直线的斜率为正值,
故为![]() .
.


科目:高中数学 来源: 题型:
【题目】对于函数y=f(x),若在其定义域内存在x0,使得x0f(x0)=1成立,则称函数f(x)具有性质M.
(1)下列函数中具有性质M的有____
①f(x)=﹣x+2
②f(x)=sinx(x∈[0,2π])
③f(x)=x![]() ,(x∈(0,+∞))
,(x∈(0,+∞))
④f(x)![]()
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则实数a的取值范围是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
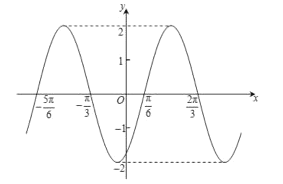
【题目】函数![]() 的图象如图所示,为了得到函数
的图象如图所示,为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象( )
的图象( )
A.先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的
个单位,再把所得各点的横坐标伸长到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
B.先向左平移![]() 个单位,再把所得各点的横坐标缩短到原来的
个单位,再把所得各点的横坐标缩短到原来的![]() (纵坐标不变)
(纵坐标不变)
C.每个点的横坐标缩短到原来的![]() (纵坐标不变),再向左平移
(纵坐标不变),再向左平移![]() 个单位
个单位
D.每个点的横坐标伸长到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校高一年级某研究小组经过调查发现:提高北环隧道的车辆通行能力可有效改善交通状况,在一般情况下,隧道内的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米,车流密度指每千米道路上车辆的数量)的函数.当隧道内的车流密度达到210辆/千米时,将造成堵塞,此时车流速度为0;当车流密度不超过30辆/千米时,车流速度为60千米/小时,研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)求函数![]() 的表达式;
的表达式;
(2)当车流密度为多大时,车流量(单位时间内通过某观测点的车辆数,单位:辆/小时) ![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面a内作菱形ABCD,边长为1,∠BAD=60°,再在a的上方,分别以△ABD与△CBD为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.

(1)求二面角P-BD-Q的余弦值;
(2)求点P到平面QBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系,将曲线![]() 上的每一个点的横坐标保持不变,纵坐标缩短为原来的
上的每一个点的横坐标保持不变,纵坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,
轴的正半轴为极轴,建立极坐标系, ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的参数方程;
的参数方程;
(Ⅱ)过原点![]() 且关于
且关于![]() 轴对称的两条直线
轴对称的两条直线![]() 与
与![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() ,且点
,且点![]() 在第一象限,当四边形
在第一象限,当四边形![]() 的周长最大时,求直线
的周长最大时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com