
【题目】函数![]() ,
,![]() .
.
(Ⅰ)讨论![]() 的极值点的个数;
的极值点的个数;
(Ⅱ)若对于![]() ,总有
,总有![]() .(i)求实数
.(i)求实数![]() 的范围; (ii)求证:对于
的范围; (ii)求证:对于![]() ,不等式
,不等式![]() 成立.
成立.
【答案】见解析.
【解析】【试题分析】(Ⅰ)先运用求导法则求函数的导数,再分类进行探求; (Ⅱ)先将不等式进行等价转化,再构造函数借助导数的有关知识进行推证:
(Ⅰ)解法一:由题意得![]() , 令
, 令![]()
(1)当![]() ,即
,即![]() 时,
时,![]() 对
对![]() 恒成立
恒成立
即![]() 对
对![]() 恒成立,此时
恒成立,此时![]() 没有极值点;…………2分
没有极值点;…………2分
(2)当![]() ,即
,即![]()
①![]() 时,设方程
时,设方程![]() 两个不同实根为
两个不同实根为![]() ,不妨设
,不妨设![]()
则![]() ,故
,故![]()
∴![]() 时
时![]() ;在
;在![]() 时
时![]()
故![]() 是函数
是函数![]() 的两个极值点.
的两个极值点.
②![]() 时,设方程
时,设方程![]() 两个不同实根为
两个不同实根为![]() ,
,
则![]() ,故
,故![]()
∴![]() 时,
时,![]() ;故函数
;故函数![]() 没有极值点. ……………………………4分
没有极值点. ……………………………4分
综上,当![]() 时,函数
时,函数![]() 有两个极值点;
有两个极值点;
当![]() 时,函数
时,函数![]() 没有极值点. ………………………………………5分
没有极值点. ………………………………………5分
解法二:![]() , …………………………………………1分
, …………………………………………1分
![]() ,
,
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 对
对![]() 恒成立,
恒成立,![]() 在
在![]() 单调增,
单调增,![]() 没有极值点; ……………………………………………………………3分
没有极值点; ……………………………………………………………3分
②当![]() ,即
,即![]() 时,方程
时,方程![]() 有两个不等正数解
有两个不等正数解![]() ,
,
![]()
不妨设![]() ,则当
,则当![]() 时,
时,![]() 增;
增;![]() 时,
时,![]() 减;
减;![]() 时,
时,![]() 增,所以
增,所以![]() 分别为
分别为![]() 极大值点和极小值点,
极大值点和极小值点,![]() 有两个极值点.
有两个极值点.
综上所述,当![]() 时,
时,![]() 没有极值点;
没有极值点;
当![]() 时,
时,![]() 有两个极值点. ………………………………5分
有两个极值点. ………………………………5分
(Ⅱ)(i)![]() ,
,
由![]() ,即
,即![]() 对于
对于![]() 恒成立,设
恒成立,设![]() ,
,
![]() ,
,
![]() ,
,![]() 时,
时,![]() 减,
减,![]() 时,
时,![]() 增,
增,
![]() ,
,![]() . ……………………………………9分
. ……………………………………9分
(ii)由(i)知,当![]() 时有
时有![]() ,即:
,即:![]() ,
,![]() ……①当且仅当
……①当且仅当![]() 时取等号, ……………………………10分
时取等号, ……………………………10分
以下证明:![]() ,设
,设![]() ,
,![]() ,
,
![]() 当
当![]() 时
时![]() 减,
减,![]() 时
时![]() 增,
增,
![]() ,
,![]() ,……②当且仅当
,……②当且仅当![]() 时取等号;
时取等号;
由于①②等号不同时成立,故有![]() .……………………………12分
.……………………………12分


科目:高中数学 来源: 题型:
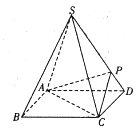
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,P为侧棱SD上的点,且
倍,P为侧棱SD上的点,且![]() .
.
(1)求二面角![]() 的大小;
的大小;
(2)在侧棱SC上是否存在一点E,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:
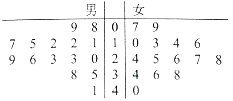
若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
(1)将频率视为概率,估计该校900名学生中“读书迷”有多少人?
(2)从已抽取的7名“读书迷”中随机抽取男、女“读书迷”各1人,参加读书日宣传活动.
(i)共有多少种不同的抽取方法?
(ii)求抽取的男、女两位“读书迷”月均读书时间相差不超过2小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市2017年3月1日至16日的空气质量指数趋势图,空气质量指数![]() 小于
小于![]() 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于![]() 表示空气重度污染.
表示空气重度污染.
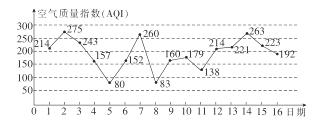
(1)若该人随机选择3月1日至3月14日中的某一天到达该市,到达后停留![]() 天(到达当日算
天(到达当日算![]() 天),求此人停留期间空气重度污染的天数为
天),求此人停留期间空气重度污染的天数为![]() 天的概率;
天的概率;
(2)若该人随机选择3月7日至3月12日中的![]() 天到达该市,求这
天到达该市,求这![]() 天中空气质量恰有
天中空气质量恰有![]() 天是重度污染的概率.
天是重度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
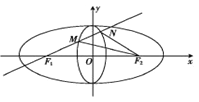
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的.如图,椭圆![]() 与椭圆
与椭圆![]() 是相似的两个椭圆,并且相交于上下两个顶点.椭圆
是相似的两个椭圆,并且相交于上下两个顶点.椭圆![]() 的长轴长是4,椭圆
的长轴长是4,椭圆![]() 短轴长是1,点
短轴长是1,点![]() 分别是椭圆
分别是椭圆![]() 的左焦点与右焦点.
的左焦点与右焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com