练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线上一点到焦点的距离为，过作两条互相垂直的直线和，其中斜率为与抛物线交于A，B，与y轴交于C，点Q满足：

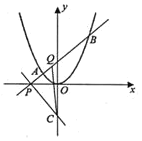
    （1）求抛物线的方程；

    （2）求三角形PQC面积的最小值.

    【答案】（1）； （2）

    【解析】

    （1）根据抛物线定义，到焦点的距离等于到其准线的距离，求得抛物线方程；

    （2）应用设而不解，联立方程组，根与系数的关系，以及向量式，将点的纵坐标均用表示出来，再表示出，从而表示出三角形的面积，再求最值.

    解：（1）抛物线化为标准方程为：，其准线为，

    则，得,故抛物线的方程为.

    （2）由题,，则，

    设，则，得，

    则，.

    由,则,得,

    ,则,得,

    故,得

    又,,则,

    ,

    又, 令，

    则

    则在递减，在递增，

    故当时，的最小值为，

    故三角形PQC面积的最小值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下面给出有关的四个论断：①；②；③或；④.以其中的三个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：若______，则_______（用序号表示）并给出证明过程：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表为年至年某百货零售企业的线下销售额（单位：万元），其中年份代码年份．

    年份代码

    线下销售额

    （1）已知与具有线性相关关系，求关于的线性回归方程，并预测年该百货零售企业的线下销售额；

    （2）随着网络购物的飞速发展，有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑，某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法，随机调查了位男顾客、位女顾客（每位顾客从“持乐观态度”和“持不乐观态度”中任选一种），其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有人、女顾客有人，能否在犯错误的概率不超过的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关？

    参考公式及数据：．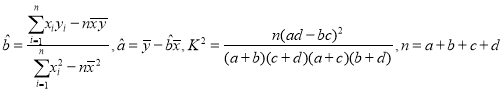

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆Γ：的左，右焦点分别为F1(，0)，F2(，0)，椭圆的左，右顶点分别为A，B，已知椭圆Γ上一异于A，B的点P，PA，PB的斜率分别为k1，k2，满足.

    （1）求椭圆Γ的标准方程；

    （2）若过椭圆Γ左顶点A作两条互相垂直的直线AM和AN，分别交椭圆Γ于M，N两点，问x轴上是否存在一定点Q，使得∠MQA=∠NQA成立，若存在，则求出该定点Q，否则说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本（万元）与年产量（吨）之间的函数关系式可以近似的表示为，已知此生产线年产量最大为吨．

    （1）求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；

    （2）若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥，底面为正方形，且底面，过的平面与侧面的交线为，且满足（表示的面积）.

    （1）证明： 平面；

    （2）当时，二面角的余弦值为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的顶点在坐标原点，准线方程为，为抛物线的焦点，点为直线上任意一点，以为圆心，为半径的圆与抛物线的准线交于、两点，过、分别作准线的垂线交抛物线于点、.

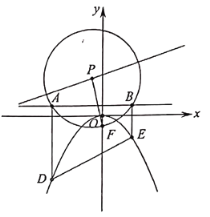
    （1）求抛物线的方程；

    （2）证明：直线过定点，并求出定点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一款小游戏的规则如下：每轮游戏要进行三次，每次游戏都需要从装有大小相同的2个红球，3个白球的袋中随机摸出2个球，若摸出的“两个都是红球”出现3次获得200分，若摸出“两个都是红球”出现1次或2次获得20分，若摸出“两个都是红球”出现0次则扣除10分（即获得分）．

    （1）设每轮游戏中出现“摸出两个都是红球”的次数为，求的分布列；

    （2）玩过这款游戏的许多人发现，若干轮游戏后，与最初的分数相比，分数没有增加反而减少了，请运用概率统计的相关知识分析解释上述现象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知项数为的数列满足如下条件：①；②若数列满足其中则称为的“伴随数列”.

    （I）数列是否存在“伴随数列”，若存在，写出其“伴随数列”；若不存在，请说明理由；

    （II）若为的“伴随数列”，证明：；

    （III）已知数列存在“伴随数列”且求的最大值.

    查看答案和解析>>

    同步练习册答案