练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在三棱柱中，侧棱与底面垂直， ，点分别为和的中点.

    （1）证明： 平面；

    证明： 平面.

    【答案】（1）见解析（2）见解析

    【解析】试题分析：（1）先证明平面，从而可得，再由正方形的性质可得进而根据线面垂直的判定定理可得结果；（2）连接由题意可知，点分别为和的中点，由中位线定理可得，根据线面平行的判定定理可得结果.

    证明：（1）由题设可知， 平面面， ，

    又

    平面

    平面平面

    又因四边形为正方形， 为的中点，

    平面平面平面；

    （2）连接由题意可知，点分别为和的中点，

    又平面平面平面

    【方法点晴】本题主要考查线面垂直、线面平行的判定定理以及空间想象能力，属于难题.证明直线和平面垂直的常用方法有：（1）利用判定定理；（2）利用判定定理的推论；（3）利用面面平行的性质；（4）利用面面垂直的性质，当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当x∈[1，4]时，求函数的值域；

    （2）如果对任意的x∈[1，4]，不等式恒成立，求实数k的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC.E是PC的中点，作EF⊥PB交PB于点F.

    （1)证明PA∥平面EDB；

    （2)证明PB⊥平面EFD；

    （3)求二面角C－PB－D的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4－1《几何证明选讲》

    已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

    （1）求证:BD平分∠ABC;

    （2）若AB=4,AD=6,BD=8,求AH的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】上饶某中学研究性学习小组为调查市民喜欢观看体育节目是否与性别有关，随机抽取了55名市民，得数据如下表：

    喜欢

    不喜欢

    合计

    男

    20

    5

    25

    女

    10

    20

    30

    合计

    30

    25

    55

    （1）判断是否有99.5%的把握认为喜欢观看体育节目与性别有关？

    （2）用分层抽样的方法从喜欢观看体育节目的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求男市民人数的分布列和期望．

    下面的临界值表供参考：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】上周某校高三年级学生参加了数学测试，年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩（均为整数）的频率分布直方图如图所示.

    （Ⅰ）估计这次月考数学成绩的平均分和众数；

    （Ⅱ）假设抽出学生的数学成绩在段各不相同，且都超过94分.若将频率视为概率，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数字中任意抽取2个数，有放回地抽取3次，记这3次抽取中恰好有两名学生的数学成绩的次数为，求的分布列和期望.

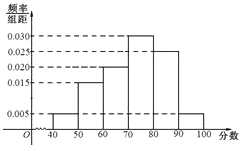
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在原点，焦点在轴上，离心率为，右焦点到右顶点的距离为．

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）是否存在与椭圆交于两点的直线：，使得成立？若存在，求出实数的取值范围，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业．根据规划，本年度投入万元，以后每年投入将比上年减少．本年度当地旅游业收入估计为万元，由于该项建设对旅游业的促进作用，预计今后的旅游业收入每年会比上年增加．

    （Ⅰ）设年内（本年度为第一年）总投入为万元，旅游业总收入为万元．写出的表达式；

    （Ⅱ）至少经过几年旅游业的总收入才能超过总投入?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C所对的边分别是a，b，c已知b=4，c=5，A=60°．
    （1）求边长a和△ABC的面积；
    （2）求sin2B的值．

    查看答案和解析>>

    同步练习册答案