
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.
(Ⅰ)M为曲线C1上的动点,点P在线段OM上,且满足|OM||OP|=16,求点P的轨迹C2的直角坐标方程;
(Ⅱ)设点A的极坐标为(2, ![]() ),点B在曲线C2上,求△OAB面积的最大值.
),点B在曲线C2上,求△OAB面积的最大值.
【答案】解:(Ⅰ)曲线C1的直角坐标方程为:x=4,
设P(x,y),M(4,y0),则 ![]() ,∴y0=
,∴y0= ![]() ,
,
∵|OM||OP|=16,
∴ ![]() =16,
=16,
即(x2+y2)(1+ ![]() )=16,
)=16,
整理得:(x﹣2)2+y2=4(x≠0),
∴点P的轨迹C2的直角坐标方程:(x﹣2)2+y2=4(x≠0).
(Ⅱ)点A的直角坐标为A(1, ![]() ),显然点A在曲线C2上,|OA|=2,
),显然点A在曲线C2上,|OA|=2,
∴曲线C2的圆心(2,0)到弦OA的距离d= ![]() =
= ![]() ,
,
∴△AOB的最大面积S= ![]() |OA|(2+
|OA|(2+ ![]() )=2+
)=2+ ![]() .
.
【解析】(Ⅰ)设P(x,y),利用相似得出M点坐标,根据|OM||OP|=16列方程化简即可;
(Ⅱ)求出曲线C2的圆心和半径,得出B到OA的最大距离,即可得出最大面积.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x﹣cos2x﹣2 ![]() sinx cosx(x∈R).
sinx cosx(x∈R).
(Ⅰ)求f( ![]() )的值.
)的值.
(Ⅱ)求f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10 ![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(Ⅰ)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(Ⅱ)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,右顶点为点
,右顶点为点![]() .
.
(1)若直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 两点(
两点(![]() 不是左、右顶点),且
不是左、右顶点),且![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(2)![]() 是椭圆
是椭圆![]() 的两个动点,若直线
的两个动点,若直线![]() 的斜率与
的斜率与![]() 的斜率互为相反数,试判断直线EF的斜率是否为定值?如果是,求出定值;反之,请说明理由.
的斜率互为相反数,试判断直线EF的斜率是否为定值?如果是,求出定值;反之,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,两个顶点分别为
,两个顶点分别为![]() ,
,![]() .过点
.过点![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 的交点为
的交点为![]() .
.
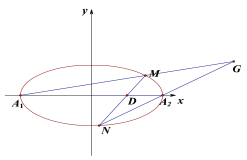
(1)求椭圆的标准方程;
(2)求证:点![]() 在一条定直线上.
在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() 是角
是角![]() 的对边,则其中真命题的序号是__________.
的对边,则其中真命题的序号是__________.
①若![]() ,则
,则![]() 在
在![]() 上是增函数;
上是增函数;
②若![]() ,则
,则![]() 是直角三角形;
是直角三角形;
③![]() 的最小值为
的最小值为![]() ;
;
④若![]() ,则
,则![]() ;
;
⑤若![]() ,则
,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com