
【题目】已知二次函数![]() .
.
(Ⅰ)若![]() 的最大值为
的最大值为![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)对于任意的![]() ,总有
,总有![]() .求实数
.求实数![]() 的取值范围;
的取值范围;
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】
(Ⅰ) 设![]() ,
,![]() 转化为二次函数
转化为二次函数![]() 在
在![]() 的最值,由二次函数图象性质可知此最大值只能是
的最值,由二次函数图象性质可知此最大值只能是![]() 之一,通过讨论,即可求出a;
之一,通过讨论,即可求出a;
(Ⅱ)令t=sinxcosx,变量分离转化为关于t的二次函数的最值,通过恒成立求出a的取值范围.
解:(Ⅰ)二次函数中![]()
设![]() ∴
∴![]() ,若
,若![]() (
(![]() )的最大值为
)的最大值为![]()
即关于S的二次函数![]() 在区间上
在区间上![]() 有最大值
有最大值![]() ,
,
由二次函数图象性质可知此最大值只能是![]() 之一
之一
若![]() ,此时二次函数开口向下且对称轴
,此时二次函数开口向下且对称轴![]() ,所以函数在区间上最大值在顶点处取得,不是
,所以函数在区间上最大值在顶点处取得,不是![]() ,不合题意;
,不合题意;
若![]() ,此时二次函数开口向上且对称轴
,此时二次函数开口向上且对称轴![]() ,最大值
,最大值![]() ,符合题意
,符合题意
若![]() ,此时二次函数开口向下且对称轴
,此时二次函数开口向下且对称轴![]() ,并不在顶点处有最大值,不符合题意
,并不在顶点处有最大值,不符合题意
综上所述![]() .
.
(Ⅱ)![]() 对于任意的
对于任意的![]() ,总有
,总有![]() ,
,
令![]() ,
,
则命题转化为![]() ,不等式
,不等式![]() 恒成立,
恒成立,
当![]() 时,
时,![]() 使
使![]() 成立;
成立;
当![]() 时,有
时,有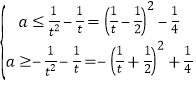
对于任意的![]() 恒成立;
恒成立;
∵![]() ∴
∴![]() 或
或![]() ,则
,则![]() ,故要使①式成立,
,故要使①式成立,
则有![]() ,又
,又![]() ,故要使②式成立,则有
,故要使②式成立,则有![]() ,由题设知
,由题设知![]() .
.
综上,![]() 为所求。
为所求。


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=lnx,其中e为自然对数的底数.
,g(x)=lnx,其中e为自然对数的底数.
(1)求函数y=f(x)g(x)在x=1处的切线方程;
(2)若存在x1 , x2(x1≠x2),使得g(x1)﹣g(x2)=λ[f(x2)﹣f(x1)]成立,其中λ为常数,求证:λ>e;
(3)若对任意的x∈(0,1],不等式f(x)g(x)≤a(x﹣1)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
(Ⅰ)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+a)﹣x,a∈R.
(1)当a=﹣1时,求f(x)的单调区间;
(2)若x≥1时,不等式ef(x)+ ![]() x2>1恒成立,求实数a的取值范围.
x2>1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是
A. 命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;
”;
B. 命题“![]() ”的否定是“
”的否定是“![]() ”;
”;
C. 命题“若x=y,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
D. “![]() ” 是“
” 是“![]() ”的必要不充分条件.
”的必要不充分条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点![]() 且互相垂直的两条直线分别与圆
且互相垂直的两条直线分别与圆![]() 交于点A,B,与圆
交于点A,B,与圆![]() 交于点C,D.
交于点C,D.

(1) 若AB=![]() ,求CD的长;
,求CD的长;
(2)若直线![]() 斜率为2,求
斜率为2,求![]() 的面积;
的面积;
(3) 若CD的中点为E,求△ABE面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com