
【题目】在平面直角坐标系xOy中,过点![]() 且互相垂直的两条直线分别与圆
且互相垂直的两条直线分别与圆![]() 交于点A,B,与圆
交于点A,B,与圆![]() 交于点C,D.
交于点C,D.

(1) 若AB=![]() ,求CD的长;
,求CD的长;
(2)若直线![]() 斜率为2,求
斜率为2,求![]() 的面积;
的面积;
(3) 若CD的中点为E,求△ABE面积的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]() .
.
【解析】
(1)分析直线斜率是否存在,当斜率存在时,利用圆中半弦长,半径,弦心距构成直角三角形求解即可(2)直线![]() 斜率为2,则直线
斜率为2,则直线![]() 方程为
方程为![]() ,求出弦长,点M到直线的距离,利用三角形面积公式求解即可(3)表示出△ABE的面积S=
,求出弦长,点M到直线的距离,利用三角形面积公式求解即可(3)表示出△ABE的面积S=![]() AB·d=2
AB·d=2![]() ,令
,令![]() ,换元后根据二次函数求最值即可.
,换元后根据二次函数求最值即可.
(1) 由题可知,直线AB斜率显然存在,设为k,则直线AB:y=kx+1.
因为O点到直线AB的距离d1=![]() ,
,
∴![]() +
+![]() =4,
=4,
∴AB=2![]()
由2![]() =
=![]() 得k2=15.
得k2=15.
因为直线AB与直线CD互相垂直,则直线CD:y=![]() x+1,
x+1,
∴M点到直线CD的距离d2=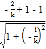 ,
,
∴![]() =1-
=1-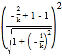 ,CD=2
,CD=2![]() =2
=2![]() =
=![]() .
.
(2) 直线![]() 斜率为2,则直线
斜率为2,则直线![]() 方程为
方程为![]()
![]() 到直线
到直线![]() 距离为
距离为![]() 到直线
到直线![]() 距离为
距离为![]()
![]()
![]()
(3)当直线AB的斜率不存在时,△ABE的面积S=![]() ×4×2=4;
×4×2=4;
当直线AB的斜率存在时,设为k,则直线AB:y=kx+1,k≠0,直线CD:y=-![]() x+1.
x+1.
由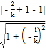 <1得k2>3, 所以k∈(-∞,-
<1得k2>3, 所以k∈(-∞,-![]() )∪(
)∪(![]() ,+∞).
,+∞).
因为![]() +
+![]() =4,所以AB=2
=4,所以AB=2![]() .
.
因为E点到直线AB的距离即M点到直线AB的距离d=![]() =
=![]() ,
,
所以△ABE的面积S=![]() AB·d=2
AB·d=2![]() .
.
令![]() ,则S=
,则S=![]()
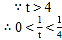
![]() ∈
∈![]() .
.
综上,△ABE面积的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知命题p:(x-2)(x+m)≤0,q:x2+(1-m)x-m≤0.
(1)若m=3,命题“p∧q”为真命题,求实数x的取值范围.
(2)若p是q的必要不充分条件,求实数m的取范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是![]()
![]()
A. 至少有一个白球;都是白球 B. 至少有一个白球;至少有一个红球
C. 至少有一个白球;红、黑球各一个 D. 恰有一个白球;一个白球一个黑球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义下凸函数如下:设f(x)为区间I上的函数,若对任意的x1 , x2∈I总有f( ![]() )≥
)≥ ![]() ,则称f(x)为I上的下凸函数,某同学查阅资料后发现了下凸函数有如下判定定理和性质定理: 判定定理:f(x)为下凸函数的充要条件是f″(x)≥0,x∈I,其中f″(x)为f(x)的导函数f′(x)的导数.
,则称f(x)为I上的下凸函数,某同学查阅资料后发现了下凸函数有如下判定定理和性质定理: 判定定理:f(x)为下凸函数的充要条件是f″(x)≥0,x∈I,其中f″(x)为f(x)的导函数f′(x)的导数.
性质定理:若函数f(x)为区间I上的下凸函数,则对I内任意的x1 , x2 , …,xn , 都有 ![]() ≥f(
≥f( ![]() ).
).
请问:在△ABC中,sinA+sinB+sinC的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=atanx+bx3+cx(a、b、c∈R),选取a、b、c的一组值计算f(1)、f(﹣1),所得出的正确结果可能是( )
A.2和1
B.2和0
C.2和﹣1
D.2和﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站观测点记录的连续4天里,AQI指数M与当天的空气水平可见度y(单位cm)的情况如下表1:
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
哈尔滨市某月AQI指数频数分布如下表2:
M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设x= ![]() ,根据表1的数据,求出y关于x的回归方程; (参考公式:
,根据表1的数据,求出y关于x的回归方程; (参考公式: ![]() ;其中
;其中 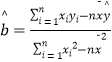 ,
, ![]() )
)
(2)小张开了一家洗车店,经统计,当M不高于200时,洗车店平均每天亏损约2000元;当M在200至400时,洗车店平均每天收入约4000元;当M大于400时,洗车店平均每天收入约7000元;根据表2估计小张的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆心角为![]() ,半径为
,半径为![]() 的扇形铁皮上截取一块矩形材料
的扇形铁皮上截取一块矩形材料![]() ,其中点
,其中点![]() 为圆心,点
为圆心,点![]() 在圆弧上,点
在圆弧上,点![]() 在两半径上,现将此矩形铁皮
在两半径上,现将此矩形铁皮![]() 卷成一个以
卷成一个以![]() 为母线的圆柱形铁皮罐的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形铁皮罐的侧面(不计剪裁和拼接损耗),设矩形的边长![]() ,圆柱形铁皮罐的容积为
,圆柱形铁皮罐的容积为![]() .
.

(1)求圆柱形铁皮罐的容积![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)当![]() 为何值时,才使做出的圆柱形铁皮罐的容积
为何值时,才使做出的圆柱形铁皮罐的容积![]() 最大?最大容积是多少? (圆柱体积公式:
最大?最大容积是多少? (圆柱体积公式:![]() ,
,![]() 为圆柱的底面枳,
为圆柱的底面枳,![]() 为圆柱的高)
为圆柱的高)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,以x轴非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的参数方程为![]() (θ为参数),直线l的极坐标方程为ρcos
(θ为参数),直线l的极坐标方程为ρcos![]() =2
=2![]() .
.
(1)写出曲线C的普通方程和直线l的直角坐标方程;
(2)求曲线C上的点到直线l的最大距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com