
已知定义在区间 上的函数y=f(x)的图象关于直线x=-
上的函数y=f(x)的图象关于直线x=- 对称,当x∈
对称,当x∈ 时,函数f(x)=Asin(ωx+φ)
时,函数f(x)=Asin(ωx+φ)  的图象如图所示.
的图象如图所示.
(1)求函数y=f(x)在 上的表达式;
上的表达式;
(2)求方程f(x)= 的解.
的解.
(1)
(2)x=-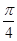 或-
或- 或-
或- 或
或 .
.
解析试题分析:解:(1)当x∈ 时,A=1,
时,A=1, =
= -
- ,T=2π,ω=1.
,T=2π,ω=1.
且f(x)=sin(x+φ)过点 ,
,
则 +φ=π,φ=
+φ=π,φ=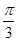 .
.
f(x)=sin .
.
当-π≤x<- 时,-
时,- ≤-x-
≤-x-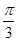 ≤
≤ ,
,
f =sin
=sin ,
,
而函数y=f(x)的图象关于直线x=- 对称,
对称,
则f(x)=f ,
,
即f(x)=sin =-sin x,-π≤x<-
=-sin x,-π≤x<- .
.
∴
(2)当- ≤x≤
≤x≤ 时,
时, ≤x+
≤x+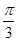 ≤π,
≤π,
由f(x)=sin =
= ,
,
得x+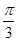 =
=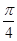 或
或 ,x=-
,x=- 或
或 .
.
当-π≤x<- 时,由f(x)=-sin x=
时,由f(x)=-sin x= ,sin x=-
,sin x=- ,
,
得x=-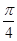 或-
或- .
.
∴x=-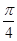 或-
或- 或-
或- 或
或 .
.
考点:三角函数的图像与解析式
点评:解决的关键是根据三角函数的性质来结合图像来得到参数的求解,同事解三角方程,属于基础题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
函数 的最小值是
的最小值是 ,在一个周期内图象最高点与最低点横坐标差是
,在一个周期内图象最高点与最低点横坐标差是 ,又:图象过点
,又:图象过点 ,
,
求(1)函数解析式,
(2)函数的最大值、以及达到最大值时 的集合;
的集合;
(3)该函数图象可由 的图象经过怎样的平移和伸缩得到?
的图象经过怎样的平移和伸缩得到?
(4)当 时,函数的值域.
时,函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数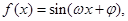 其中
其中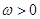 ,
,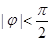
(I)若 求
求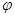 的值;
的值;
(Ⅱ)在(I)的条件下,若函数 的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于 ,求函数
,求函数 的解析式;并求最小正实数
的解析式;并求最小正实数 ,使得函数
,使得函数 的图像象左平移
的图像象左平移 个单位所对应的函数是偶函数。
个单位所对应的函数是偶函数。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
已知函数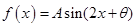 ,其中
,其中 请分别解答以下两小题.
请分别解答以下两小题.
(Ⅰ)若函数过点 ,求函数
,求函数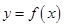 的解析式.
的解析式.
(Ⅱ)如图,点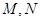 分别是函数
分别是函数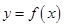 的图像在
的图像在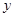 轴两侧与
轴两侧与 轴的两个相邻交点, 函数图像上的一点
轴的两个相邻交点, 函数图像上的一点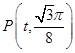 ,若满足
,若满足 ,求函数
,求函数 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com