
【题目】已知在梯形![]() 中,
中, ![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)连接![]() 交
交![]() 于点
于点![]() ,利用平几知识可得
,利用平几知识可得![]() ,再根据相似比得
,再根据相似比得![]() .最后根据线面平行判定定理得
.最后根据线面平行判定定理得![]() 平面
平面![]() .(2)求二面角大小,一般利用空间向量数量积:先根据条件建立空间直角坐标系,设立各点坐标,列方程组求各平面法向量,利用向量数量积求两法向量夹角,最后根据二面角与法向量夹角关系求二面角.
.(2)求二面角大小,一般利用空间向量数量积:先根据条件建立空间直角坐标系,设立各点坐标,列方程组求各平面法向量,利用向量数量积求两法向量夹角,最后根据二面角与法向量夹角关系求二面角.
试题解析:解: (Ⅰ)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,如图①所示.
,如图①所示.
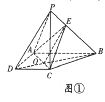
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() 平面
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)设![]() ∵
∵![]() 且
且![]() 平面
平面![]() ,故以
,故以![]() 为原点,过点
为原点,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,
轴,
![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系如图②所示,则
轴,建立空间直角坐标系如图②所示,则

![]() .
.
由![]() ,得
,得![]() ,得
,得![]() .
.
解得![]() ,即
,即![]() ,
,
![]() .
.
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则![]()
令![]() ,则
,则![]() ,即
,即![]() .
.
取![]() 的中点,记为
的中点,记为![]() ,连接
,连接![]() ,
,
易求得![]() 的坐标为
的坐标为![]() ,
,
∴![]()
![]() .
.
由![]() ,得
,得![]() ,
,
由![]() 底面
底面![]() ,得
,得![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() .
.
∴![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
∴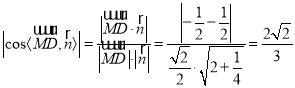 .
.
由图可知二面角![]() 为锐二面角,
为锐二面角,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(1)根据上表数据,请在如图坐标系中画出散点图; 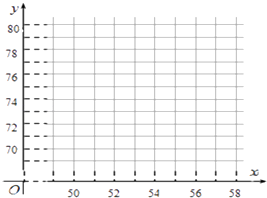
(2)根据上表数据,用最小二乘法求出y关于x的线性回归方程 ![]() ;(保留2位小数)
;(保留2位小数)
(3)若周六同一时间段车流量是25万辆,试根据(2)求出的线性回归方程预测,此时PM2.5的浓度为多少(保留整数)?
参考公式: ![]() =
= 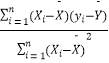 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见表.
例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.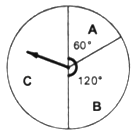
(1)已知顾客甲消费后获得n次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为p,每次转动转盘的结果相互独立,设ξ为顾客甲转动转盘指针落在区域边界的次数,ξ的数学期望Eξ= ![]() ,方差Dξ=
,方差Dξ= ![]() ,求n、p的值;
,求n、p的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为η(元).求随机变量η的分布列和数学期望.
指针位置 | A区域 | B区域 | C区域 |
返券金额(单位:元) | 60 | 30 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2﹣a2x+3.
(1)若a=2,求f(x)在[﹣1,2]上的最值;
(2)若f(x)在(﹣ ![]() ,1)上是减函数,求a的取值范围.
,1)上是减函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)= 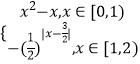 ,若x∈[﹣4,﹣2)时,f(x)≥
,若x∈[﹣4,﹣2)时,f(x)≥ ![]() 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )
A.[﹣2,0)∪(0,1)
B.[﹣2,0)∪[1,+∞)
C.[﹣2,1]
D.(﹣∞,﹣2]∪(0,1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com