
【题目】设数列![]() 的首项
的首项![]() ,且
,且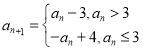 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅱ)若![]() ,证明:
,证明:![]() .
.
(Ⅲ)若![]() ,求所有的正整数
,求所有的正整数![]() ,使得对于任意
,使得对于任意![]() ,均有
,均有![]() 成立.
成立.
【答案】详见解析
【解析】
试题(I)由a1=a且0<a<1代入得到a2;a2∈(3,4),代入(2)得到a3;a3∈(0,1),代入(1)得a4;a4∈(3,4),代入(2)得到a4;a5∈(0,1),代入(1)所以求得a5;
(II)分两种情况①当0<an≤3时和②当3<an<4得到0<an+1<4得证;
(III)分三种情况若0<a<1;1≤a<2;若a=2,由特殊值得到k的特值,写出k的一般的取值即可.
试题解析:
(Ⅰ)∵![]() 得
得![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() .
.
(Ⅱ)证明:①当![]() 时,
时,![]() ,∴
,∴![]() ,
,
②当![]() ,
,![]() ,∴
,∴![]() ,
,
综上,![]() 时,
时,![]() .
.
(Ⅲ)①若![]() ,由Ⅰ知
,由Ⅰ知![]() ,所以
,所以![]() ,
,
∴ 当![]() 时,对所有的
时,对所有的![]() ,
,![]() 成立.
成立.
②若![]() ,则
,则![]() ,且
,且![]() ,
,
![]() ,∴
,∴![]() ,
,
∴ 当![]() 时,对所有的
时,对所有的![]() ,
,![]() 成立,
成立,
③若![]() ,则
,则![]() ,∴
,∴![]() ,
,
∴ ![]() 时,对所有的
时,对所有的![]() ,
,![]() 成立,
成立,
综上,若![]() ,则
,则![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,PD//MA,MA⊥AD,PM⊥平面CDM,MA=AD![]() PD=1.
PD=1.
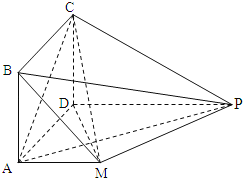
(1)求证:平面ABCD⊥平面AMPD;
(2)求三棱锥A﹣CMP的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() (
(![]() )的顶点,且椭圆与双曲线的离心率互为倒数.
)的顶点,且椭圆与双曲线的离心率互为倒数.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设动点![]() ,
, ![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,记直线
,记直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】富华中学的一个文学兴趣小组中,三位同学张博源、高家铭和刘雨恒分别从莎士比亚、雨果和曹雪芹三位名家中选择了一位进行性格研究,并且他们选择的名家各不相同.三位同学一起来找图书管理员刘老师,让刘老师猜猜他们三人各自的研究对象.刘老师猜了三句话:“①张博源研究的是莎士比亚;②刘雨恒研究的肯定不是曹雪芹;③高家铭自然不会研究莎士比亚.”很可惜,刘老师的这种猜法,只猜对了一句.据此可以推知张博源、高家铭和刘雨恒分别研究的是__________.(A莎士比亚、B雨果、C曹雪芹,按顺序填写字母即可.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com