
【题目】已知函数f(x)=![]() x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函数f(x)的定义域;
(2)讨论函数f(x)的奇偶性;
(3)求a的取值范围,使f(x)>0在定义域上恒成立.
【答案】(1){x|x∈R,且x≠0}(2)偶函数(3)a>1.
【解析】
(1)由于ax-1≠0,则ax≠1,所以x≠0,
所以函数f(x)的定义域为{x|x∈R,且x≠0}.
(2)对于定义域内任意的x,有
f(-x)=![]() (-x)3=-
(-x)3=-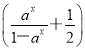 x3=-
x3=-![]() x3=
x3=![]() x3=f(x)所以f(x)是偶函数.
x3=f(x)所以f(x)是偶函数.
(3)①当a>1时,对x>0,
所以ax>1,即ax-1>0,所以![]() +
+![]() >0.
>0.
又x>0时,x3>0,所以x3![]() >0,
>0,
即当x>0时,f(x)>0.
由(2)知,f(x)是偶函数,即f(-x)=f(x),
则当x<0时,-x>0,有f(-x)=f(x)>0成立.
综上可知,当a>1时,f(x)>0在定义域上恒成立.
②当0<a<1时,f(x)=![]() ,
,
当x>0时,0<ax<1,此时f(x)<0,不满足题意;
当x<0时,-x>0,有f(-x)=f(x)<0,也不满足题意.
综上可知,所求a的取值范围是a>1


科目:高中数学 来源: 题型:
【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() ;
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】恩施州某电影院共有1000个座位,票价不分等次,根据电影院的经营经验,当每张票价不超过10元时、票可全部售出;当票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收入,需要给电影院一个合适的票价,基本条件是:①为了方便找零和算账,票价定为1元的整数倍.②影院放映一场电影的成本是4000元,票房收入必须高于成本,用x(元)表示每张票价,用y(元)表示该电影放映一场的纯收入(除去成本后的收入).
(1)求函数y=f(x)的解析式;
(2)票价定为多少时,电影放映一场的纯收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次人才招聘会上,有![]() 、
、![]() 两家公司分别开出了他们的工资标准:
两家公司分别开出了他们的工资标准:![]() 公司允诺第一个月工资为8000元,以后每年月工资比上一年月工资增加500元;
公司允诺第一个月工资为8000元,以后每年月工资比上一年月工资增加500元;![]() 公司允诺第一年月工资也为8000元,以后每年月工资在上一年的月工资基础上递增
公司允诺第一年月工资也为8000元,以后每年月工资在上一年的月工资基础上递增![]() ,设某人年初被
,设某人年初被![]() 、
、![]() 两家公司同时录取,试问:
两家公司同时录取,试问:
(1)若该人分别在![]() 公司或
公司或![]() 公司连续工作
公司连续工作![]() 年,则他在第
年,则他在第![]() 年的月工资分别是多少;
年的月工资分别是多少;
(2)该人打算连续在一家公司工作10年,仅从工资收入总量较多作为应聘的标准(不计其他因素),该人应该选择哪家公司,为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 平面上有一点列
平面上有一点列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,对每个正整数
,对每个正整数![]() ,点
,点![]() 位于函数
位于函数![]()
![]() 的图像上,且点
的图像上,且点![]() 、点
、点![]() 与点
与点![]() 构成一个以
构成一个以![]() 为顶角顶点的等腰三角形;
为顶角顶点的等腰三角形;
(1)求点![]() 的纵坐标
的纵坐标![]() 的表达式;
的表达式;
(2)若对每个自然数![]() ,以
,以![]() 、
、![]() 、
、![]() 为边长能构成一个三角形,求
为边长能构成一个三角形,求![]() 的取值范围;
的取值范围;
(3)设![]()
![]() ,若
,若![]() 取(2)中确定的范围内的最小整数,问数列
取(2)中确定的范围内的最小整数,问数列![]() 的最大项的项数是多少?试说明理由;
的最大项的项数是多少?试说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆中心在原点,焦点在![]() 轴上,
轴上,![]()
![]() 为椭圆长轴的两个端点,
为椭圆长轴的两个端点,![]() 为椭圆的右焦点.已知椭圆的离心率为
为椭圆的右焦点.已知椭圆的离心率为![]() ,且
,且![]() .
.

(1)求椭圆的标准方程;
(2)设![]() 是椭圆上位于
是椭圆上位于![]() 轴上方的一个动点,直线
轴上方的一个动点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过原点
经过原点![]() 且与直线
且与直线![]() 相切于点
相切于点![]()
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)在圆![]() 上是否存在两点
上是否存在两点![]() 关于直线
关于直线![]() 对称,且以线段
对称,且以线段![]() 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线![]() 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com