
【题目】已知![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若![]() 存在两个极值点
存在两个极值点![]() 且
且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)首先,函数的定义域为![]() ,然后求函数的导数
,然后求函数的导数![]() ,最后分
,最后分![]() 和
和![]() 两种情况讨论
两种情况讨论![]() 的解集,得到函数的单调区间;(Ⅱ)首先求函数的导数
的解集,得到函数的单调区间;(Ⅱ)首先求函数的导数![]() ,然后分
,然后分![]() 和
和![]() 两种情况讨论函数的极值点,借助二次方程根与系数的关系,化简
两种情况讨论函数的极值点,借助二次方程根与系数的关系,化简![]() ,通过换元
,通过换元![]() 将问题转化为函数
将问题转化为函数![]() <0,求
<0,求![]() 的取值范围,即求函数的导数,判定定义域内的单调性,求函数的最值,判断函数的最大值是否小于0,求
的取值范围,即求函数的导数,判定定义域内的单调性,求函数的最值,判断函数的最大值是否小于0,求![]() 的取值范围.
的取值范围.
试题解析:(1)由已知得![]() ,
,
①若![]() 时,由
时,由![]() ,得:
,得:![]() ,恒有
,恒有![]() ,
,
∴![]() 在
在![]() 递增;
递增;
②若![]() ,由
,由![]() ,得:
,得:![]() ,恒有
,恒有![]() ,
,
∴![]() 在
在![]() 递减;
递减;
综上,![]() 时,
时,![]() 在
在![]() 递增,
递增,
![]() 时,
时,![]() 在
在![]() 递减;
递减;
(2)![]() ,
,
∴![]() ,
,
令![]() ,
,![]() 时,
时,![]() 无极值点,
无极值点,
![]() 时,令
时,令![]() 得:
得:![]() 或
或![]() ,
,
由![]() 的定义域可知
的定义域可知![]() 且
且![]() ,
,
∴![]() 且
且![]() ,解得:
,解得:![]() ,
,
∴![]() 为
为![]() 的两个极值点,
的两个极值点,
即![]()
且![]() ,得:
,得:
![]()
=![]() ,
,
令![]() ,
,
①![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 递减,
递减,![]() ,
,
即![]() 时,
时,![]() 成立,符合题意;
成立,符合题意;
②![]() 时,
时,![]() ,∴
,∴![]() ,
,
∴![]() 在(0,1)递减,
在(0,1)递减,![]() ,
,
∴![]() 时,
时,![]() ,不合题意,
,不合题意,
综上,![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,正四棱锥![]() 中底面边长为
中底面边长为![]() ,侧棱PA与底面ABCD所成角的正切值为
,侧棱PA与底面ABCD所成角的正切值为![]() .
.
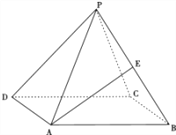
(I)求正四棱锥![]() 的外接球半径;
的外接球半径;
(II)若![]() 是
是![]() 中点,求异面直线
中点,求异面直线![]() 与
与![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3名志愿者在10月1号至10月5号期间参加社区服务工作.
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记![]() 表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
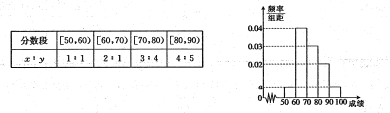
【题目】某校100名学生其中考试语文成绩的频率分布直方图所示,其中成绩分组区间是:
![]() .
.
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,
之比如下表所示,
求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]()
(1) 判别函数f(x)的奇偶性;
(2) 判断函数f(x)的单调性,并根据函数单调性的定义证明你的判断正确;
(3) 求关于x的不等式f(1-x2)+f(2x+2)<0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位: ![]() )满足关系
)满足关系![]() ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值。
达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 40 | 18 | 58 |
大于40岁 | 15 | 27 | 42 |
总计 | 55 | 45 | 100 |
(1)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(2)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com