
【题目】已知椭圆的一个顶点为A(0,﹣1),焦点在x轴上.若右焦点到直线x﹣y+2 ![]() =0的距离为3.
=0的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线y=kx+m(k≠0)相交于不同的两点M、N.当|AM|=|AN|时,求m的取值范围.
【答案】
(1)解:依题意可设椭圆方程为 ![]() ,
,
则右焦点F( ![]() )由题设
)由题设 ![]()
解得a2=3故所求椭圆的方程为 ![]() ;
;
(2)解:设P为弦MN的中点,由 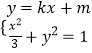
得(3k2+1)x2+6mkx+3(m2﹣1)=0
由于直线与椭圆有两个交点,∴△>0,即m2<3k2+1①
∴ ![]() 从而
从而 ![]()
∴ ![]() 又|AM|=||AN|,∴AP⊥MN,
又|AM|=||AN|,∴AP⊥MN,
则 ![]() 即2m=3k2+1②
即2m=3k2+1②
把②代入①得2m>m2解得0<m<2由②得 ![]() 解得
解得 ![]() .
.
故所求m的取范围是( ![]() ).
).
【解析】(1)依题意可设椭圆方程为 ![]() ,由题设
,由题设 ![]() 解得a2=3,故所求椭圆的方程为
解得a2=3,故所求椭圆的方程为 ![]() .(2)设P为弦MN的中点,由
.(2)设P为弦MN的中点,由 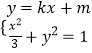 得(3k2+1)x2+6mkx+3(m2﹣1)=0,由于直线与椭圆有两个交点,∴△>0,即m2<3k2+1.由此可推导出m的取值范围.
得(3k2+1)x2+6mkx+3(m2﹣1)=0,由于直线与椭圆有两个交点,∴△>0,即m2<3k2+1.由此可推导出m的取值范围.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,A(2,4),B(﹣1,2),C,D为动点,
(1)若C(3,1),求平行四边形ABCD的两条对角线的长度
(2)若C(a,b),且 ![]() ,求
,求 ![]() 取得最小值时a,b的值.
取得最小值时a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的程序框图表示的算法中,输入三个实数a,b,c,要求输出的x是这三个数中最大的数,那么在空白的判断框中,应该填入( ) 
A.x>c
B.c>x
C.c>b
D.c>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}和等比数列{bn},其中{an}的公差不为0.设Sn是数列{an}的前n项和.若a1 , a2 , a5是数列{bn}的前3项,且S4=16.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{ ![]() }为等差数列,求实数t;
}为等差数列,求实数t;
(3)构造数列a1 , b1 , a2 , b1 , b2 , a3 , b1 , b2 , b3 , …,ak , b1 , b2 , …,bk , …,若该数列前n项和Tn=1821,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1的左右焦点分别为F1 , F2 , 则在椭圆C上满足∠F1PF2=
=1的左右焦点分别为F1 , F2 , 则在椭圆C上满足∠F1PF2= ![]() 的点P的个数有( )
的点P的个数有( )
A.0个
B.1个
C.2 个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点. 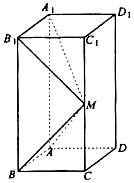
(1)证明:B1M⊥平面ABM;
(2)求异面直线A1M和C1D1所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(1, ![]() )是函数f(x)=
)是函数f(x)= ![]() ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足
ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足 ![]() =
= ![]() +1(n≥2). (Ⅰ)求数列{an}的通项公式;
+1(n≥2). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{ ![]() }的前n项和为Tn , 问使Tn>
}的前n项和为Tn , 问使Tn> ![]() 的最小正整数n是多少?
的最小正整数n是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥 ![]() 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形, ![]() ,
, ![]() ,平面
,平面 ![]() 底面ABCD, O为AD的中点, M是棱PC上的点, AD=2AB.
底面ABCD, O为AD的中点, M是棱PC上的点, AD=2AB.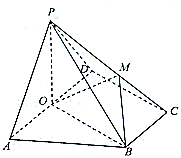
(1)求证:平面 ![]() 平面PAD;
平面PAD;
(2)若 ![]() 平面BMO,求
平面BMO,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com