Question

【题目】设函数．

（1）关于的不等式对一切恒成立，求实数的取值范围；

（2）解关于的不等式；

（3）函数在区间上有零点，求实数的取值范围．

Answer 1

【答案】（1）；（2）见解析；（3）.

【解析】

（1）对一切恒成立，即，恒成立，所以，解得即可；

（2）对判别式讨论大于0，等于0，小于0，再由二次不等式的解法，即可得到；

（3）要使函数在有零点，只需考虑的符号和对称轴的位置及端点的函数值的符号以及零点存在定理和运用，列出不等式组，解出即可得到范围．

（1）由题意得，对一切恒成立，

即，恒成立，

所以，即，

解得，，

所以实数的取值范围；

（2）由，得，，

即，

其中，

当即时，不等式无实数解；

当，即或时，

设，，

则，

综上所述，当时，不等式无解；

当或时，不等式的解集为；

（3）要使函数在区间上上有零点，

须或，或，

即或，

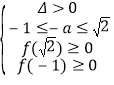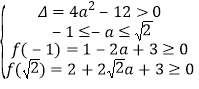解得，或，

综上所述，实数的取值范围．