
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且满足
上,且满足![]() .
.

(1)求证:![]() ;
;
(2)在棱![]() 上确定一点
上确定一点![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,并求此时
四点共面,并求此时![]() 的长;
的长;
(3)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题本题有两种方法,第一种是传统方法:(1)连接![]() ,先由正方体的性质得到
,先由正方体的性质得到![]() ,以及
,以及![]() 平面
平面![]() ,从而得到
,从而得到![]() ,利用直线与平面垂直的判定定理可以得到
,利用直线与平面垂直的判定定理可以得到![]() 平面
平面![]() ,于是得到
,于是得到![]() ;(2)假设四点
;(2)假设四点![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,利用平面与平面平行的性质定理得到
四点共面,利用平面与平面平行的性质定理得到![]() ,
,![]() ,于是得到四边形
,于是得到四边形![]() 为平行四边形,从而得到
为平行四边形,从而得到![]() 的长度,再结合勾股定理得到
的长度,再结合勾股定理得到![]() 的长度,最终得到
的长度,最终得到![]() 的长度;(3)先延长
的长度;(3)先延长![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() ,找出由平面
,找出由平面![]() 与平面
与平面![]() 所形成的二面角的棱
所形成的二面角的棱![]() ,借助
,借助![]() 平面
平面![]() ,从点
,从点![]() 在平面
在平面![]() 内作
内作![]() ,连接
,连接![]() ,利用三垂线法得到
,利用三垂线法得到![]() 为平面
为平面![]() 与平面
与平面![]() 所形成的二面角的的平面角,然后在直角
所形成的二面角的的平面角,然后在直角![]() 中计算
中计算![]() 的余弦值;
的余弦值;
第二种方法是空间向量法:(1)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,确定
轴建立空间直角坐标系,确定![]() 与
与![]() 的坐标,利用
的坐标,利用![]() 来证明
来证明![]() ,进而证明
,进而证明![]()
![]() ;(2)先利用平面与平面平行的性质定理得到
;(2)先利用平面与平面平行的性质定理得到![]() ,然后利用空间向量共线求出点
,然后利用空间向量共线求出点![]() 的坐标,进而求出
的坐标,进而求出![]() 的长度;(3)先求出平面
的长度;(3)先求出平面![]() 和平面
和平面![]() 的法向量,结合图形得到由平面
的法向量,结合图形得到由平面![]() 和平面
和平面![]() 所形成的二面角为锐角,最后再利用两个平面的法向量的夹角来进行计算.
所形成的二面角为锐角,最后再利用两个平面的法向量的夹角来进行计算.
试题解析:(1)如下图所示,连接![]() ,
,
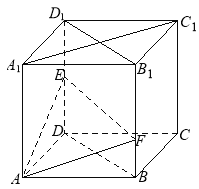
由于![]() 为正方体,所以四边形
为正方体,所以四边形![]() 为正方形,所以
为正方形,所以![]() ,
,
且![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ;
;
(2)如下图所示,假设![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,则
四点共面,则![]() 、
、![]() 、
、![]() 、
、![]() 四点确定平面
四点确定平面![]() ,
,
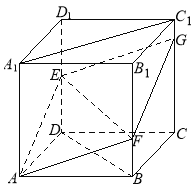
由于![]() 为正方体,所以平面
为正方体,所以平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
由平面与平面平行的判定定理得![]() ,
,
同理可得![]() ,因此四边形
,因此四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得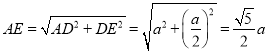 ,
,
在直角梯形![]() 中,下底
中,下底![]() ,直角腰
,直角腰![]() ,斜腰
,斜腰![]() ,
,
由勾股定理可得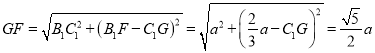 ,
,
结合图形可知![]() ,解得
,解得![]() ;
;
(3)延长![]() 、
、![]() ,设
,设![]() ,连接
,连接![]() ,则
,则![]() 是平面
是平面![]() 与平面
与平面![]() 的交线,
的交线,
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() 为平面
为平面![]() 与平面
与平面![]() 所成二面角的平面角,
所成二面角的平面角,
因为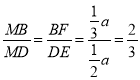 ,即
,即![]() ,因此
,因此![]() ,
,
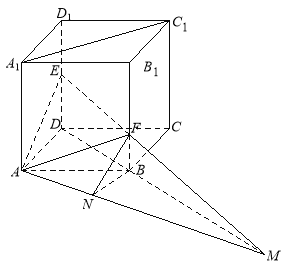
在![]() 中,
中,![]() ,
,![]() ,
,
所以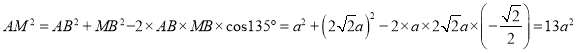 ,
,
即![]() ,
,
因为![]() ,
,
所以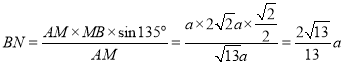 ,
,
所以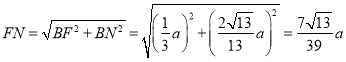 ,
,
所以![]() ,故平面
,故平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() .
.
空间向量法:
(1)证明:以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如下图所示的空间直角坐标系,则
轴,建立如下图所示的空间直角坐标系,则![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
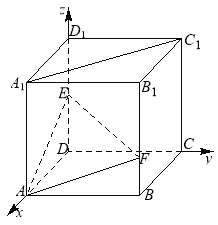
所以![]() ,
,![]() ,因为
,因为![]() ,
,
所以![]() ,所以
,所以![]() ;
;
(2)设![]() ,因为平面
,因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以存在实数![]() ,使得
,使得![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() ,
,
故当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共面;
四点共面;
(3)由(1)知![]() ,
,![]() ,
,
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则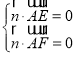 ,即
,即 ,
,
取![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
而![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ,
,
则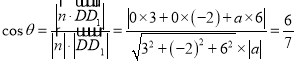 ,
,
故平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() ;
;
第(1)、(2)问用推理论证法,第(3)问用空间向量法,
(1)、(2)给分同推理论证法.
(3)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]()


科目:高中数学 来源: 题型:
【题目】某市为了缓解城市交通压力,大力发展公共交通,提倡多坐公交少开车,为了调查市民乘公交车的候车情况,交通主管部门从在某站台等车的![]() 名候车乘客中随机抽取
名候车乘客中随机抽取![]() 人,按照他们的候车时间(单位:分钟)作为样本分成
人,按照他们的候车时间(单位:分钟)作为样本分成![]() 组,如下表所示:
组,如下表所示:
组别 | 一 | 二 | 三 | 四 | 五 | 六 |
候车时间 |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
(1)估计这![]() 名乘客中候车时间少于
名乘客中候车时间少于![]() 分钟的人数;
分钟的人数;
(2)若从上表第四、五组的![]() 人中随机抽取
人中随机抽取![]() 人做进一步的问卷调查,求抽到的
人做进一步的问卷调查,求抽到的![]() 人恰好来自不同组的概率.
人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(1)求m的值并写出曲线C的直角坐标方程;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某工厂![]() 和
和![]() 两车间工人掌握某技术情况,现从这两车间工人中分别抽查
两车间工人掌握某技术情况,现从这两车间工人中分别抽查![]() 名和
名和![]() 名工人,经测试,将这
名工人,经测试,将这![]() 名工人的测试成绩编成的茎叶图。若成绩在
名工人的测试成绩编成的茎叶图。若成绩在![]() 以上(包括
以上(包括![]() )定义为“良好”,成绩在
)定义为“良好”,成绩在![]() 以下定义为“合格”。已知
以下定义为“合格”。已知![]() 车间工人的成绩的平均数为
车间工人的成绩的平均数为![]() ,
,![]() 车间工人的成绩的中位数为
车间工人的成绩的中位数为![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 车间工人的成绩的方差;
车间工人的成绩的方差;
(3)在这![]() 名工人中,用分层抽样的方法从 “良好”和“及格”中抽取
名工人中,用分层抽样的方法从 “良好”和“及格”中抽取![]() 人,再从这
人,再从这![]() 人中选
人中选![]() 人,求至少有一人为“良好”的概率。
人,求至少有一人为“良好”的概率。
(参考公式:方差![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则下面的四个值中不为定值的是( ) 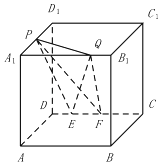
A.点Q到平面PEF的距离
B.直线PE与平面QEF所成的角
C.三棱锥P﹣QEF的体积
D.二面角P﹣EF﹣Q的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义[x]表示不超过的最大整数,如[2]=2,[2,2]=2,执行如图所示的程序框图,则输出S=( ) 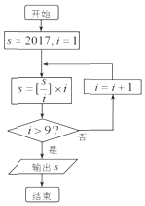
A.1991
B.2000
C.2007
D.2008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)若二面角E﹣BD﹣P大于60°,求四棱锥P﹣ABCD体积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com