
【题目】椭圆 ![]() 的离心率为
的离心率为 ![]() ,右焦点到直线
,右焦点到直线 ![]() 的距离为
的距离为 ![]() ,过M(0,﹣1)的直线l交椭圆于A,B两点.
,过M(0,﹣1)的直线l交椭圆于A,B两点.
(1)求椭圆的方程;
(2)若直线l交x轴于N, ![]() ,求直线l的方程.
,求直线l的方程.
【答案】
(1)解:设右焦点为(c,0)(c>0)
∵右焦点到直线 ![]() 的距离为
的距离为 ![]() ,
,
∴ ![]()
∴ ![]()
∵椭圆 ![]() 的离心率为
的离心率为 ![]() ,
,
∴ ![]()
∴ ![]()
∴ ![]()
∴椭圆的方程为 ![]() ;
;
(2)解:设A (x1,y1),B(x2,y2),N(x0,0)
∵ ![]() ,
,
∴ ![]() x2﹣x0,y2)
x2﹣x0,y2)
∴ ![]() ①
①
易知直线斜率不存在时或斜率为0时①不成立
于是设直线l的方程为y=kx﹣1(k≠0).
与椭圆方程联立 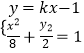 ,消去x可得(4k2+1)y2+2y+1﹣8k2=0②
,消去x可得(4k2+1)y2+2y+1﹣8k2=0②
∴ ![]() ③
③ ![]() ④
④
由①③可得 ![]() ,
, ![]() 代入④整理可得:8k4+k2﹣9=0
代入④整理可得:8k4+k2﹣9=0
∴k2=1
此时②为5y2+2y﹣7=0,判别式大于0
∴直线l的方程为y=±x﹣1
【解析】(1)根据右焦点到直线 ![]() 的距离为
的距离为 ![]() ,可得
,可得 ![]() ,利用椭圆
,利用椭圆 ![]() 的离心率为
的离心率为 ![]() ,可得
,可得 ![]() ,从而可得
,从而可得 ![]() ,
, ![]() ,故可求椭圆的方程;(2)设A (x1 , y1),B(x2 , y2),N(x0 , 0),利用
,故可求椭圆的方程;(2)设A (x1 , y1),B(x2 , y2),N(x0 , 0),利用 ![]() ,可得
,可得 ![]() x2﹣x0 , y2),设直线l的方程为y=kx﹣1(k≠0).与椭圆方程联立
x2﹣x0 , y2),设直线l的方程为y=kx﹣1(k≠0).与椭圆方程联立 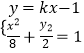 ,消去x可得(4k2+1)y2+2y+1﹣8k2=0,由此即可求得直线l的方程.
,消去x可得(4k2+1)y2+2y+1﹣8k2=0,由此即可求得直线l的方程.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】如图,PD⊥平面ABCD,DC⊥AD,BC∥AD,PD:DC:BC=1:1: ![]() .
. 
(1)若AD=DC,求异面直线PA,BC所成的角;
(2)求PB与平面PDC所成角大小;
(3)求二面角D﹣PB﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数x、y、m满足|x﹣m|>|y﹣m|,则称x比y远离m.
(1)若x2﹣1比3远离0,求x的取值范围;
(2)对任意两个不相等的正数a、b,证明:a3+b3比a2b+ab2远离2ab ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a﹣2)x+a﹣4;
(1)若函数y=f(x)在区间[1,2]上的最小值为4﹣a,求实数a的取值范围;
(2)是否存在整数m,n,使得关于x的不等式m≤f(x)≤n的解集恰好为[m,n],若存在,求出m,n的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=x,过点M(2,0)作直线l:x=ny+2与抛物线C交于A,B两点,点N是定直线x=﹣2上的任意一点,分别记直线AN,MN,BN的斜率为k1 , k2 , k3 .
(1)求 ![]() 的值;
的值;
(2)试探求k1 , k2 , k3之间的关系,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知离心率为 ![]() 的椭圆C:
的椭圆C: ![]() +
+ ![]() =1(a>b>0)过点M(2,1),O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A、B.
=1(a>b>0)过点M(2,1),O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A、B. 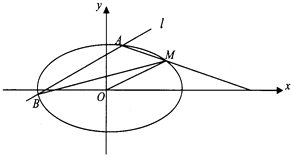
(1)求椭圆C的方程.
(2)证明:直线MA、MB与x轴围成一个等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为 ![]() ,且过点D(2,0).
,且过点D(2,0).
(1)求该椭圆的标准方程;
(2)设点 ![]() ,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga|x+1|(a>0且a≠1),当x∈(0,1)时,恒有f(x)<0成立,则函数g(x)=loga(﹣ ![]() x2+ax)的单调递减区间是 .
x2+ax)的单调递减区间是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com