
【题目】已知函数f(x)=loga|x+1|(a>0且a≠1),当x∈(0,1)时,恒有f(x)<0成立,则函数g(x)=loga(﹣ ![]() x2+ax)的单调递减区间是 .
x2+ax)的单调递减区间是 .
【答案】(0,![]() ]
]
【解析】解:由题意:当x∈(0,1)时,|x+1|>1,但loga|x+1|<0,故由对数函数的图象知,0<a<1;
∵对数函数的真数要大于0,即﹣ ![]() x2+ax>0,解得:0<x<
x2+ax>0,解得:0<x< ![]() a,
a,
令t=﹣ ![]() x2+ax,开口向下,对称轴x=
x2+ax,开口向下,对称轴x= ![]() ,
,
当x在(0, ![]() ]时增函数,x在[
]时增函数,x在[ ![]() ,
, ![]() )时减函数.
)时减函数.
根据复合函数的单调性“同增异减”可得:
x∈(0,1)时,恒有f(x)<0成立时,函数g(x)=loga(﹣ ![]() x2+ax)的单调递减区间是(0,
x2+ax)的单调递减区间是(0, ![]() ].
].
所以答案是:(0, ![]() ].
].
【考点精析】关于本题考查的复合函数单调性的判断方法,需要了解复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”才能得出正确答案.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的离心率为
的离心率为 ![]() ,右焦点到直线
,右焦点到直线 ![]() 的距离为
的距离为 ![]() ,过M(0,﹣1)的直线l交椭圆于A,B两点.
,过M(0,﹣1)的直线l交椭圆于A,B两点.
(1)求椭圆的方程;
(2)若直线l交x轴于N, ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本公司计划2009年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(已知幂函数f(x)=x ![]() ,(k∈Z)满足f(2)<f(3).
,(k∈Z)满足f(2)<f(3).
(1)求实数k的值,并求出相应的函数f(x)解析式;
(2)对于(1)中的函数f(x),试判断是否存在正数q,使函数g(x)=1﹣qf(x)+(2q﹣1)x在区间[﹣1,2]上值域为 ![]() .若存在,求出此q.
.若存在,求出此q.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,PA=AD=AB=2BC,M,N分别为PC,PB的中点. (Ⅰ)求证:PB⊥DM;
(Ⅱ)求CD与平面ADMN所成的角的正弦值.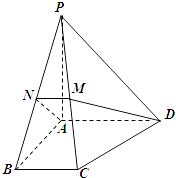
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】P是双曲线 ![]() =1(a>0,b>0)上的点,F1、F2是其焦点,且
=1(a>0,b>0)上的点,F1、F2是其焦点,且 ![]() =0,若△F1PF2的面积是9,a+b=7,则双曲线的离心率为( )
=0,若△F1PF2的面积是9,a+b=7,则双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知底面为边长为2的正方形,侧棱长为1的直四棱柱ABCD﹣A1B1C1D1中,P是面A1B1C1D1上的动点.给出以下四个结论中,正确的个数是( ) ①与点D距离为 ![]() 的点P形成一条曲线,则该曲线的长度是
的点P形成一条曲线,则该曲线的长度是 ![]() ;
;
②若DP∥面ACB1 , 则DP与面ACC1A1所成角的正切值取值范围是 ![]() ;
;
③若 ![]() ,则DP在该四棱柱六个面上的正投影长度之和的最大值为
,则DP在该四棱柱六个面上的正投影长度之和的最大值为 ![]() .
.
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com