练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数定义域为，部分对应值如表，的导函数的图象如图所示. 下列关于函数的结论正确的有（ ）

    A.函数的极大值点有个

    B.函数在上是减函数

    C.若时，的最大值是，则的最大值为4

    D.当时，函数有个零点

    【答案】ABD

    【解析】

    利用导函数的图象可判断A、B选项的正误；取，结合函数的最值与单调性的关系可判断C选项的正误；作出函数的草图，数形结合可判断D选项的正误.综合可得出结论.

    由导数的正负性可知，函数的单调递增区间为、，单调递减区间为、，B选项正确；

    函数有个极大值点，A选项正确；

    当时，函数最大值是，而最大值不是，C选项错误；

    作出函数的图象如下图所示，由下图可知，当时，函数与函数的图象有四个交点，D选项正确.

    故选：ABD.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆：的离心率为，以椭圆的左顶点为圆心作圆：，设圆与椭圆交于点与点．

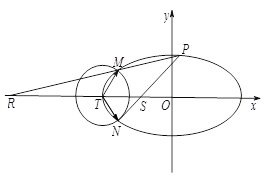
    （1）求椭圆的方程；

    （2）求的最小值，并求此时圆的方程；

    （3）设点是椭圆上异于,的任意一点，且直线分别与轴交于点，为坐标原点，

    求证：为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是菱形，侧面底面，，，为线段的中点.

    （1）求证：平面；

    （2）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个圆周上有9个点，以这9个点为顶点作3个三角形.当这3个三角形无公共顶点且边互不相交时，我们把它称为一种构图.满足这样条件的构图共有（ ）种.

    A. 3 B. 6 C. 9 D. 12

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某射手在一次射击训练中，射中10环，9环，8环、7环的概率分别是0.21，0.23，0.25，0.28，计算这个射手在一次射击中：

    （1）射中10环或7环的概率； （2）不够7环的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，设H为锐角△ABC的垂心.由顶点A向以BC为直径的⊙O作一条切线AE，切点为E，联结EH交AO于点G，过G任意作⊙O的一条弦PQ.证明：AO 平分∠PAQ.

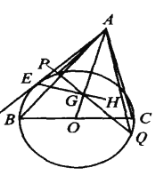
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 的内切圆切边于点， 而是边上的任意内点.设和的内切圆圆心分别是和.

    （1）求证：∠I1DI2 =90°（即、、、四点共圆）；

    （2）设、、、四点所在的圆周的半径为， 而的内切圆半径为，试求的取值范围（取遍各种形状的三角形，点取遍边上的每一个内点）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】王府井百货分店今年春节期间，消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该分店经理对春节前7天参加抽奖活动的人数进行统计， 表示第天参加抽奖活动的人数，得到统计表格如下：

    1

    2

    3

    4

    5

    6

    7

    5

    8

    8

    10

    14

    15

    17

    经过进一步统计分析，发现与具有线性相关关系．

    （1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

    （2）判断变量与之间是正相关还是负相关；

    （3）若该活动只持续10天，估计共有多少名顾客参加抽奖．

    参与公式： ， ， ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）讨论的单调性；

    （2）设函数，若有两个零点.

    （i）求的取值范围；

    （ii）证明：.

    查看答案和解析>>

    同步练习册答案