求直线a:2x+y-4=0关于直线l:3x+4y-1=0对称的直线b的方程。
答案:
解析:
| 解法一:由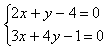
得a与l的交点E(3,-2)也在b上,
设b的斜率为k,则
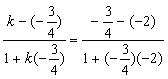
解得k=-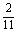 。 。
∴直线b的方程为:y-(-2)=- 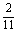 (x-3) (x-3)
即2x+11y+16=0。
解法二:在直线a:2x+y-4=0上取一点A(2,0),设A关于l的对称点B(x0,y0),
则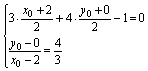
解得B(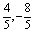 ),求得E(3,-2) ),求得E(3,-2)
∴直线b的方程为: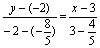
即2x+11y+16=0。
解法三:设P(x,y)是直线b上的任一点,P关于l的对称点为P′(x′,y′),
则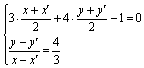
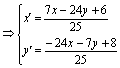
∵P′(x′,y′)在直线a:2x+y-4=0上,
∴2·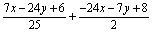 -4=0。 -4=0。
即2x+11y+16=0。
这就是所求直线b的方程。
|
