
【题目】函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() 时,
时,![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
【答案】(1)见解析
(2)![]()
【解析】
(1)对![]() 求导,再因式分解,讨论每个因式的正负,再判断
求导,再因式分解,讨论每个因式的正负,再判断![]() 的正负,进而判断
的正负,进而判断![]() 的单调性;(2)代入
的单调性;(2)代入![]() ,将不等式
,将不等式![]() 中的
中的![]() 和
和![]() 分离在不等号两边,然后讨论不等号含有
分离在不等号两边,然后讨论不等号含有![]() 一边的函数的单调性,进而判断最值,再计算
一边的函数的单调性,进而判断最值,再计算![]() 的取值范围,由
的取值范围,由![]() 是正整数的条件可求出
是正整数的条件可求出![]() 的最大值.
的最大值.
解:(1)函数![]() 的定义域为
的定义域为![]() ,
,![]()
①当![]() 时,因为
时,因为![]() ,故有
,故有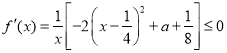 .
.
此时函数![]() 在区间
在区间![]() 单调递减.
单调递减.
②当![]() ,有
,有![]() ,方程
,方程![]() 的两根分别是:
的两根分别是:
![]()
![]() 函数
函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 函数
函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 函数
函数![]() 在
在![]() 上单调递减.
上单调递减.
③当![]() 时,易知
时,易知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减.
单调递减.
(2)当![]()
设![]()
![]() 当
当![]() 时,有
时,有![]() ,
,
设![]()
![]() 在
在![]() 上单调递增,
上单调递增,
又![]() 在
在![]() 上的函数图像是一条不间断的曲线,
上的函数图像是一条不间断的曲线,
且![]() ,
,![]()
存在唯一的![]() ,使得
,使得![]() ,即
,即![]() .
.
当![]() ;
;
当![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]()
![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]()
![]() 时,不等式
时,不等式![]() 对任意
对任意![]() 恒成立,
恒成立,
![]() 正整数
正整数![]() 的最大值是3.
的最大值是3.


科目:高中数学 来源: 题型:
【题目】为了解运动健身减肥的效果,某健身房调查了20名肥胖者,测量了他们的体重(单位:千克).健身之前他们的体重情况如三维饼图(1)所示,经过半年的健身后,他们的体重情况如三维饼图(2)所示,对比健身前后,关于这20名肥胖者,下面结论正确的是( )
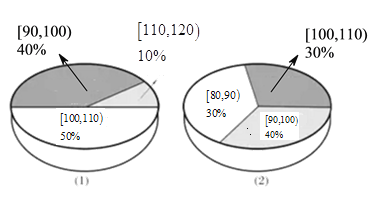
A.他们健身后,体重在区间![]() 内的人数不变
内的人数不变
B.他们健身后,体重在区间![]() 内的人数减少了2个
内的人数减少了2个
C.他们健身后,体重在区间![]() 内的肥胖者体重都有减轻
内的肥胖者体重都有减轻
D.他们健身后,这20位肥胖着的体重的中位数位于区间![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某高架桥箱梁的横截面,它由上部路面和下部支撑箱两部分组成.如图2,路面宽度![]() ,下部支撑箱CDEF为等腰梯形(
,下部支撑箱CDEF为等腰梯形(![]() ),且
),且![]() .为了保证承重能力与稳定性,需下部支撑箱的面积为
.为了保证承重能力与稳定性,需下部支撑箱的面积为![]() ,高度为2m且
,高度为2m且![]() ,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),
,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),![]() .
.

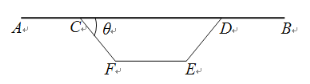
(1)试用θ表示箱梁的总造价y(千元);
(2)试确定cosθ的值,使总造价最低?并求最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜率为![]() 的直线
的直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)设点![]() 在第一象限,过
在第一象限,过![]() 作抛物线
作抛物线![]() 的准线的垂线,
的准线的垂线,![]() 为垂足,且
为垂足,且![]() ,直线
,直线![]() 与直线
与直线![]() 关于直线
关于直线![]() 对称,求直线
对称,求直线![]() 的方程;
的方程;
(2)过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() 与
与![]() 面积之和为
面积之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜率为![]() 的直线
的直线![]() 过抛物线
过抛物线![]() :
:![]() 的焦点
的焦点![]() ,且与拋物线
,且与拋物线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)设点![]() 在笫一象限,过
在笫一象限,过![]() 作拋物线
作拋物线![]() 的准线的垂线,
的准线的垂线,![]() 为垂足,且
为垂足,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() 与
与![]() 面积之和为
面积之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某中学甲、乙两班共有25名学生报名参加了一项 测试.这25位学生的考分编成的茎叶图,其中有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.

(Ⅰ)求这两个班学生成绩的中位数及x的值;
(Ⅱ)如果将这些成绩分为“优秀”(得分在175分 以上,包括175分)和“过关”,若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛,求这3人中甲班至多有一人入选的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com