【题目】2018年8月31日，十三届全国人大常委会第五次会议表决通过了关于修改个人所得税法的决定，这是我国个人所得税法自1980年出台以来第七次大修
为了让纳税人尽早享受减税红利，在过渡期对纳税个人按照下表计算个人所得税，值得注意的是起征点变为5000元，即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额．
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过3000元的部分 |
|
2 | 超过3000元至12000元的部分 |
|
3 | 超过12000元至25000元的部分 |
|
|
|
|
某企业员工今年10月份的月工资为15000元，则应缴纳的个人所得税为______元
科目：高中数学 来源： 题型：
【题目】有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩，得到如下所示的列联表：
优秀 | 非优秀 | 总计 | |
甲班 | 10 | b | |
乙班 | c | 30 | |
总计105 |
已知在全部105人中随机抽取1人，成绩优秀的概率为
，则下列说法正确的是（ ）
参考公式：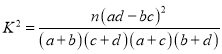
附表：
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
A.列联表中c的值为30，b的值为35
B.列联表中c的值为15，b的值为50
C.根据列联表中的数据，若按95%的可靠性要求，能认为“成绩与班级有关系”
D.根据列联表中的数据，若按95%的可靠性要求，不能认为“成绩与班级有关系”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某森林公园有一直角梯形区域ABCD，其四条边均为道路，AD∥BC，∠ADC＝90°，AB＝5千米，BC＝8千米，CD＝3千米．现甲、乙两管理员同时从
地出发匀速前往D地，甲的路线是AD，速度为6千米/小时，乙的路线是ABCD，速度为v千米/小时．
（1）若甲、乙两管理员到达D的时间相差不超过15分钟，求乙的速度v的取值范围；
（2）已知对讲机有效通话的最大距离是5千米．若乙先到达D，且乙从A到D的过程中始终能用对讲机与甲保持有效通话，求乙的速度v的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=Asin（ωx+φ），x∈R（其中A＞0，ω＞0，0＜φ
）的周期为π，且图象上的一个最低点为M（
）．
（1）求f（x）的解析式及单调递增区间；
（2）当x∈[0，
]时，求f（x）的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
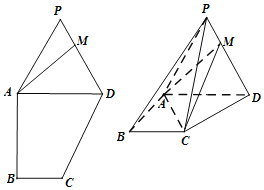
【题目】如图，在多边形PABCD中，
，
，
，
，M是线段PD上的一点，且
，若将
沿AD折起，得到几何体
．
证明：
平面AMC
若
，且平面
平面ABCD，求三棱锥
的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
、
为双曲线
的左、右焦点，过作垂直于
轴的直线，在轴上方交双曲线
于点
，且
，圆
的方程是
.
（1）求双曲线的方程；
（2）过双曲线上任意一点
作该双曲线两条渐近线的垂线，垂足分别为
、
，求
的值；
（3）过圆上任意一点
作圆的切线
交双曲线于
、
两点，
中点为，求证：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】把两个全等的正三棱锥的底面粘在一起，在所得的六面体中，所有二面角相等，而顶点可分成两类：在第一类中，每一个顶点发出三条棱；而在第二类顶点中，每一个顶点发出四条棱。试求连结两个第一类顶点的线段长与连结两个第二类顶点的线段长之比。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
