
【题目】如图,在平面直角坐标系xOy中,椭圆![]() 的离心率为
的离心率为![]() ,过椭圆右焦点
,过椭圆右焦点![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() 与
与![]() .当直线
.当直线![]() 斜率为0时,
斜率为0时,![]() .
.

(1)求椭圆的方程;
(2)求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,(2)
,(2)![]() .
.
【解析】
试题分析:(1)求椭圆标准方程,只需两个独立条件. 一个是![]() ,另一个是点
,另一个是点![]() 在椭圆上即
在椭圆上即![]() ,所以
,所以![]() .所以椭圆的方程为
.所以椭圆的方程为![]() .(2)研究直线与椭圆位置关系,关键确定参数,一般取直线的斜率,① 当两条弦中一条斜率为0时,另一条弦的斜率不存在,由题意知
.(2)研究直线与椭圆位置关系,关键确定参数,一般取直线的斜率,① 当两条弦中一条斜率为0时,另一条弦的斜率不存在,由题意知![]() ,② 当两弦斜率均存在且不为0时,设直线
,② 当两弦斜率均存在且不为0时,设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程代入椭圆方程中,并整理得
的方程代入椭圆方程中,并整理得![]() ,所以
,所以![]() .同理,
.同理,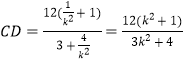 .所以
.所以![]() ,利用不等式或函数单调性可得
,利用不等式或函数单调性可得![]() 的取值范围是
的取值范围是![]() 综合①与②可知,
综合①与②可知,![]() 的取值范围是
的取值范围是![]() .
.
【解】(1)由题意知,![]() ,
,![]() ,
,
所以![]() . 2分
. 2分
因为点![]() 在椭圆上,即
在椭圆上,即![]() ,
,
所以![]() .
.
所以椭圆的方程为![]() . 6分
. 6分
(2)① 当两条弦中一条斜率为0时,另一条弦的斜率不存在,
由题意知![]() ; 7分
; 7分
② 当两弦斜率均存在且不为0时,设![]() ,
,![]() ,
,
且设直线![]() 的方程为
的方程为![]() ,
,
则直线![]() 的方程为
的方程为![]() .
.
将直线![]() 的方程代入椭圆方程中,并整理得
的方程代入椭圆方程中,并整理得![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() . 10分
. 10分
同理,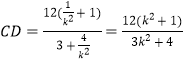 .
.
所以![]() , 12分
, 12分
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() .
.
综合①与②可知,![]() 的取值范围是
的取值范围是![]() . 16分
. 16分


科目:高中数学 来源: 题型:
【题目】去年年底,某商业集团公司根据相关评分细则,对其所属25家商业连锁店进行了考核评估.将各连锁店的评估分数按[60,70), [70,80), [80,90), [90,100),分成四组,其频率分布直方图如下图所示,集团公司依据评估得分,将这些连锁店划分为A,B,C,D四个等级,等级评定标准如下表所示.
评估得分 | [60,70) | [70,80) | [80,90) | [90,100) |
评定等级 | D | C | B | A |

(1)估计该商业集团各连锁店评估得分的众数和平均数;
(2)从评估分数不小于80分的连锁店中任选2家介绍营销经验,求至少选一家A等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C上的动点P(![]() )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为![]()
(1)求曲线C的方程。
(2)过点M(1,2)的直线![]() 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C上的动点P(![]() )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为![]()
(1)求曲线C的方程。
(2)过点M(1,2)的直线![]() 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).∠BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=3km. 
(1)求道路BE的长度;
(2)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在R上的导函数为f′(x),若f(x)<2f′(x)恒成立,且f(ln4)=2,则不等式f(x)>e ![]() 的解集是( )
的解集是( )
A.(ln2,+∞)
B.(2ln2,+∞)
C.(﹣∞,ln2)
D.(﹣∞,2ln2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com