
设椭圆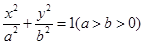 的左焦点为
的左焦点为 ,离心率为
,离心率为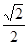 ,过点
,过点 且与
且与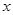 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为 .
.
(1) 求椭圆方程.
(2) 过点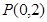 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点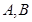 ,当
,当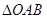 面积最大时,求
面积最大时,求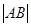 .
.
(1) 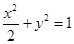 ;(2)
;(2)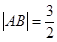 .
.
解析试题分析:(1)由离心率得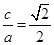 ,由过点
,由过点 且与
且与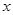 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为 得
得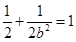 ,再加椭圆中
,再加椭圆中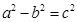 可解出
可解出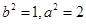 ,可得椭圆方程;(2)将直线方程设为
,可得椭圆方程;(2)将直线方程设为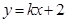 ,交点设出,然后根据题意算出
,交点设出,然后根据题意算出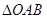 的面积
的面积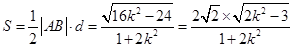 ,令
,令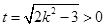 则
则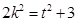 ,所以
,所以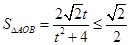 当且仅当
当且仅当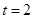 时等号成立,求出
时等号成立,求出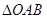 面积最大时的
面积最大时的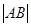 .
.
试题解析:(1)由题意可得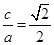 ,
,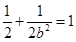 ,又
,又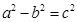 ,解得
,解得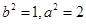 ,所以椭圆方程为
,所以椭圆方程为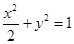 (4分)
(4分)
(2)根据题意可知,直线 的斜率存在,故设直线
的斜率存在,故设直线 的方程为
的方程为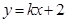 ,设
,设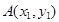 ,
,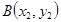 由方程组
由方程组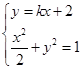 消去
消去 得关于
得关于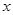 的方程
的方程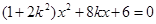 (6分)由直线
(6分)由直线 与椭圆相交于
与椭圆相交于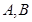 两点,则有
两点,则有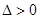 ,即
,即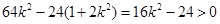 得
得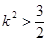
由根与系数的关系得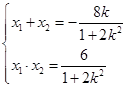
故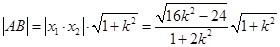 (9分)
(9分)
又因为原点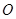 到直线
到直线 的距离
的距离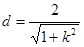 ,
,
故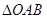 的面积
的面积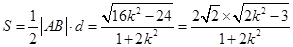
令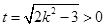 则
则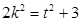 ,所以
,所以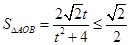 当且仅当
当且仅当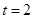 时等号成立,
时等号成立,
即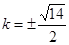 时,
时,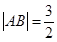 (12分)
(12分)
考点:1.椭圆方程;2.椭圆与直线综合;3.基本不等式.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
如图,在 轴上方有一段曲线弧
轴上方有一段曲线弧 ,其端点
,其端点 、
、 在
在 轴上(但不属于
轴上(但不属于 ),对
),对 上任一点
上任一点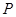 及点
及点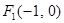 ,
,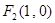 ,满足:
,满足: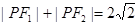 .直线
.直线 ,
,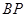 分别交直线
分别交直线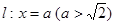 于
于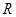 ,
,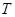 两点.
两点.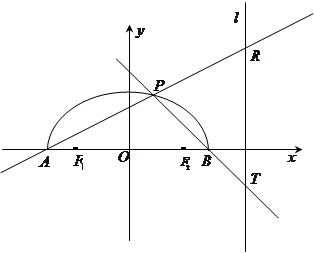
(Ⅰ)求曲线弧 的方程;
的方程;
(Ⅱ)求 的最小值(用
的最小值(用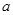 表示);
表示);
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知△ABC中, 点A,B的坐标分别为A(- ,0),B(
,0),B( ,0)点C在x轴上方.
,0)点C在x轴上方.
(Ⅰ)若点C坐标为( ,1),求以A,B为焦点且经过点C的椭圆的方程:
,1),求以A,B为焦点且经过点C的椭圆的方程:
(Ⅱ)过点P(m,0)作倾斜角为 的直线l交(1)中曲线于M,N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值.
的直线l交(1)中曲线于M,N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆的中心在原点,焦点在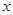 轴上,焦距为
轴上,焦距为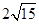 ,且经过点
,且经过点 ,直线
,直线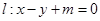 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.
(1)求 的取值范围;,
的取值范围;,
(2)若直线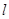 不经过点
不经过点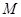 ,求证:直线
,求证:直线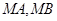 的斜率互为相反数.
的斜率互为相反数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设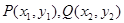 是抛物线
是抛物线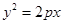
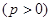 上相异两点,
上相异两点,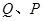 到y轴的距离的积为
到y轴的距离的积为 且
且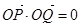 .
.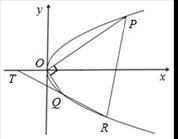
(1)求该抛物线的标准方程.
(2)过Q的直线与抛物线的另一交点为R,与 轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知,椭圆C过点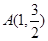 ,两个焦点为
,两个焦点为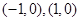 .
.
(1)求椭圆C的方程;
(2) 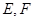 是椭圆C上的两个动点,如果直线
是椭圆C上的两个动点,如果直线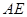 的斜率与
的斜率与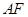 的斜率互为相反数,证明直线
的斜率互为相反数,证明直线 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆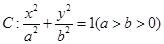 的左、右焦点分别为
的左、右焦点分别为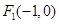 、
、 ,P为椭圆
,P为椭圆 上任意一点,且
上任意一点,且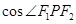 的最小值为
的最小值为 .
.
(1)求椭圆 的方程;
的方程;
(2)动圆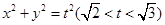 与椭圆
与椭圆 相交于A、B、C、D四点,当
相交于A、B、C、D四点,当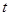 为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.
为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线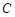 的参数方程为
的参数方程为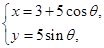
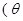 是参数
是参数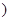 ,
,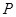 是曲线
是曲线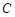 与
与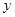 轴正半轴的交点.以坐标原点
轴正半轴的交点.以坐标原点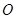 为极点,
为极点,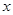 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点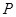 与曲线
与曲线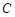 只有一个公共点的直线
只有一个公共点的直线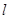 的极坐标方程.
的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com