
【题目】已知函数![]() (
(![]() ).
).
(1)讨论![]() 的单调性;
的单调性;
(2)若对![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)①当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;②当
上单调递增;②当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
(2)![]() .
.
【解析】
(1)求出函数的定义域和导函数, ![]() ,对
,对![]() 讨论,得导函数的正负,得原函数的单调性;(2)法一: 由
讨论,得导函数的正负,得原函数的单调性;(2)法一: 由![]() 得
得![]() ,
,
分别运用导函数得出函数![]() (
(![]() ),
),![]() 的单调性,和其函数的最值,可得
的单调性,和其函数的最值,可得![]() ,可得的范围;
,可得的范围;
法二:由![]() 得
得![]() ,化为
,化为![]() 令
令![]() (
(![]() ),研究函数的单调性,可得
),研究函数的单调性,可得![]() 的取值范围.
的取值范围.
(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
①当![]() 时,由
时,由![]() 得
得![]() ,
,![]() 得
得![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增;
上单调递增;
(2)法一: 由![]() 得
得![]() ,
,
令![]() (
(![]() ),则
),则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,即
,即![]() ,
,
令![]() ,
,
则![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即
,即![]() ,
,
![]() (*)
(*)
当![]() 时,
时,![]() ,
,![]() (*)式恒成立,即
(*)式恒成立,即![]() 恒成立,满足题意
恒成立,满足题意
法二:由![]() 得
得![]() ,
,![]() ,
,![]()
令![]() (
(![]() ),则
),则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,即
,即![]() ,
,
当![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() 在
在![]() 上单调递增,
上单调递增,![]() 恒成立,满足题意
恒成立,满足题意
当![]() 时,令
时,令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,使得
,使得![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,![]() ,不满足题意,
,不满足题意,
综上所述,![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】老王有一块矩形旧铁皮![]() ,其中
,其中![]() ,
,![]() ,他想充分利用这块铁皮制作一个容器,他有两个设想:设想1是沿矩形的对角线
,他想充分利用这块铁皮制作一个容器,他有两个设想:设想1是沿矩形的对角线![]() 把
把![]() 折起,使
折起,使![]() 移到
移到![]() 点,且
点,且![]() 在平面
在平面![]() 上的射影
上的射影![]() 恰好在
恰好在![]() 上,再利用新购铁皮缝制其余两个面得到一个三棱锥
上,再利用新购铁皮缝制其余两个面得到一个三棱锥![]() ;设想2是利用旧铁皮做侧面,新购铁皮做底面,缝制一个高为
;设想2是利用旧铁皮做侧面,新购铁皮做底面,缝制一个高为![]() ,侧面展开图恰为矩形
,侧面展开图恰为矩形![]() 的圆柱体;
的圆柱体;
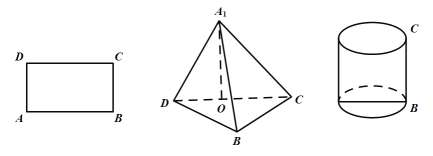
(1)求设想1得到的三棱锥![]() 中二面角
中二面角![]() 的大小;
的大小;
(2)不考虑其他因素,老王的设想1和设想2分别得到的几何体哪个容积更大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间中不同直线m、n和不同平面α、β,下面四个结论:
①若m、n互为异面直线,m∥α,n∥α,m∥β,n∥β,则α∥β;
②若m⊥n,m⊥α,n∥β,则α⊥β;
③若n⊥α,m∥α,则n⊥m;
④若α⊥β,m⊥α,n∥m,则n∥β.
其中正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代典籍《周易》用“卦”描述万物的变化,每一卦由六爻组成.其中有一种起卦方法称为“金钱起卦法”,其做法为:取三枚相同的钱币合于双手中,上下摇动数下使钱币翻滚摩擦,再随意抛撒钱币到桌面或平盘等硬物上,如此重复六次,得到六爻.若三枚钱币全部正面向上或全部反面向上,就称为变爻.若每一枚钱币正面向上的概率为![]() ,则一卦中恰有两个变爻的概率为( )
,则一卦中恰有两个变爻的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为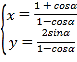 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国的嫦娥四号探测器,简称“四号星”,是世界首个在月球背面软着陆和巡视探测的航天器.2019年9月25日,中国科研人员利用嫦娥四号数据精确定位了嫦娥四号的着陆位置,并再现了嫦娥四号的落月过程,该成果由国际科学期刊《自然·通讯》在线发表.如图所示,

现假设“四号星”沿地月转移轨道飞向月球后,在月球附近一点![]() 变轨进入以月球球心
变轨进入以月球球心![]() 为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在
为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在![]() 点第二次变轨进入仍以
点第二次变轨进入仍以![]() 为一个焦点的椭圆轨道Ⅱ绕月飞行.若用
为一个焦点的椭圆轨道Ⅱ绕月飞行.若用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用
分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:①
分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的式子的序号是( )
.其中正确的式子的序号是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前n项
的前n项![]() ,
,![]() ,…,
,…,![]() 的最大项为
的最大项为![]() ,第n项之后的各项
,第n项之后的各项![]() ,
,![]() ,…的最小项为
,…的最小项为![]() ,
,![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,写出
,写出![]() ,
,![]() ,并求数列
,并求数列![]() 通项公式;
通项公式;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,判断
,判断![]() 是否为等差数列,若是,求出公差;若不是,请说明理由;
是否为等差数列,若是,求出公差;若不是,请说明理由;
(3)若数列![]() 为公差大于零的等差数列,求证:
为公差大于零的等差数列,求证:![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级有甲,乙,丙三位学生,他们前三次月考的物理成绩如表:
第一次月考物理成绩 | 第二次月考物理成绩 | 第三次月考物理成绩 | |
学生甲 | 80 | 85 | 90 |
学生乙 | 81 | 83 | 85 |
学生丙 | 90 | 86 | 82 |
则下列结论正确的是( )
A. 甲,乙,丙第三次月考物理成绩的平均数为86
B. 在这三次月考物理成绩中,甲的成绩平均分最高
C. 在这三次月考物理成绩中,乙的成绩最稳定
D. 在这三次月考物理成绩中,丙的成绩方差最大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com