练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在多面体中，底面是菱形，，，且.

    （Ⅰ）求证：；

    （Ⅱ）若平面平面，求平面与平面所成的锐二面角的余弦值.

    【答案】（Ⅰ）见解析；（Ⅱ）.

    【解析】

    （Ⅰ）取的中点，连接，，易得，接着通过证明来得到平面，进而可得结论；（Ⅱ）通过面面垂直可得平面，进而可建立如图所示的坐标系，求出平面的法向量，结合平面的一个法向量为，进而可求得最后结果.

    （Ⅰ）取的中点，连接，.∵，∴.

    ∵底面是菱形，，∴，∴，∵，∴平面.∵平面，∴.

    （Ⅱ）∵，平面平面，平面平面，∴平面.

    ∴可以为原点，，，为轴，轴，轴建立空间直角坐标系，则，，，，.

    ∴，，，∴，

    ∴，即，∴.

    设平面的一个法向量为，则

    令，则.易知平面的一个法向量为.

    设平面与平面所成的锐二面角为，∴.

    ∴平面与平面所成的锐二面角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】试求出正整数的最小可能值，使得下述命题成立：对于任意的个整数（允许相等），必定存在相应的个整数（也允许相等），且，，使得2003能整除.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线（为参数，实数），曲线（为参数，实数）.在以为极点，轴的正半轴为极轴的极坐标系中，射线与交于，两点，与交于，两点.当时，；当，.

    （1）求和的值.

    （2）求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A.离散型随机变量的方差反映了随机变量取值的波动情况；

    B.随机变量，其中越小，曲线越“矮胖”；

    C.若与是相互独立事件，则与也是相互独立事件；

    D.从10个红球和20个白球除颜色外完全相同中，一次摸出5个球，则摸到红球的个数服从超几何分布；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在直角三角形ABC中，，（如右图所示）

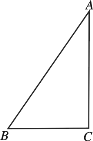
    （Ⅰ）若以AC为轴，直角三角形ABC旋转一周，试说明所得几何体的结构特征并求所得几何体的表面积.

    （Ⅱ）一只蚂蚁在问题（Ⅰ）形成的几何体上从点B绕着几何体的侧面爬行一周回到点B，求蚂蚁爬行的最短距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a，b，c分别为内角A，B，C的对边，且asin B＝－bsin.

    (1)求A；

    (2)若△ABC的面积S＝c2，求sin C的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱锥M-ABC中，MA=MB=MC=AC=，AB=BC=2，O为AC的中点，点N在边BC上，且.

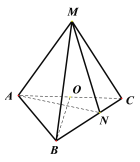
    （1）证明：BO平面AMC；

    （2）求二面角N-AM-C的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP＝AB＝AD＝1．

    （Ⅰ）若直线PB与CD所成角的大小为，求BC的长；

    （Ⅱ）求二面角B－PD－A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱中，，D为AB上一点，且平面.

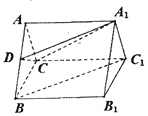
    （1）求证：；

    （2）若四边形是矩形，且平面平面ABC，直线与平面ABC所成角的正切值等于2，，，求三楼柱的体积.

    查看答案和解析>>

    同步练习册答案